-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
摘要 �hnH:�G`[F
�Y`\zLX"_m 光栅结构广泛应用于各种光学应用场景,如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM,也称为RCWA),为任意光栅结构的严格分析提供了通用和方便的工具。为此,复杂的一维或二维周期结构可以使用界面和调制介质进行配置,这允许任何类型的光栅形貌进行自由的配置。在此用例中,详细讨论了衍射级次的偏振态的研究。 h&.9�Q�{�D Mm|HA��@W^
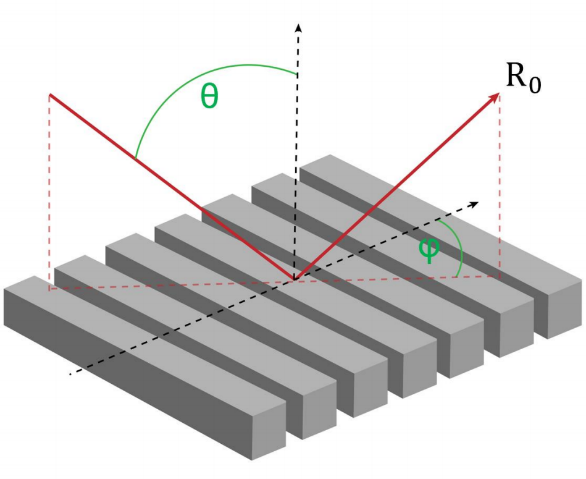 2VMa�u.eQ �7��zpw��P 任务说明 r=8]U��b�[ d$b{�KyUA
2VMa�u.eQ �7��zpw��P 任务说明 r=8]U��b�[ d$b{�KyUA 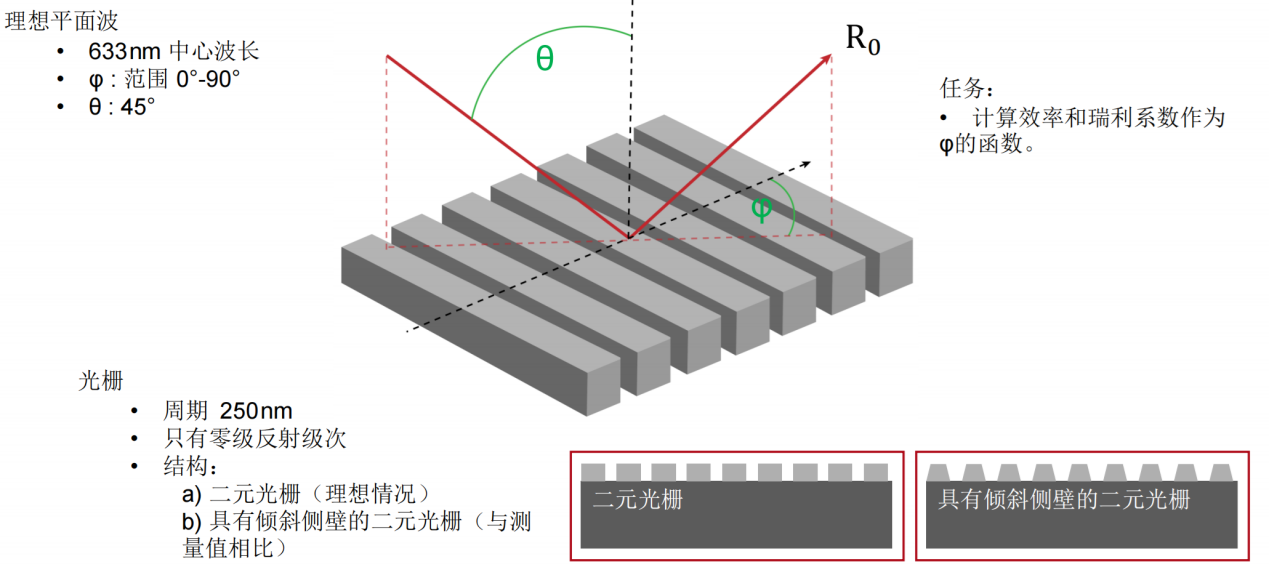 V/��J[~mN9 T�Y~0�UU�$ 简要介绍衍射效率与偏振理论 ��P?\rRB�� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 $Pl>T�09d 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: CSwNsFDR% V/��J[~mN9 T�Y~0�UU�$ 简要介绍衍射效率与偏振理论 ��P?\rRB�� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 $Pl>T�09d 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: CSwNsFDR% 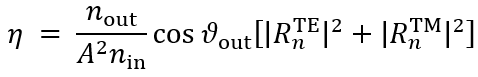 7ug�mZO}lL 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 �1rTA0�+�h 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: :��cIE8<\% 7ug�mZO}lL 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 �1rTA0�+�h 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: :��cIE8<\% 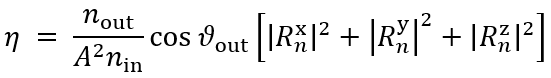 fM�
\�T�^X 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为 fM�
\�T�^X 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为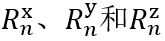 。 }evc]�?1�( >�aN@)=h}� 。 }evc]�?1�( >�aN@)=h}�
光栅结构参数 .r[J�}� O" 研究了一种矩形光栅结构。 {�I�`B?6K5 为了简化设置,选择光栅配置,只允许零阶(R_0)反射传播。 7�A�7K:,�c 根据上述参数选择以下光栅参数: 2 R���1S>X 光栅周期:250 nm �g�)xzy^2e 填充因子:0.5 ���%|�r�@q 光栅高度:200 nm M�p"��] �= 材料n_1:熔融石英(来自目录) d<f�S52~l� 材料n_2:二氧化钛(来自目录) u�&�r�@@p. !>g�c!8Y'o 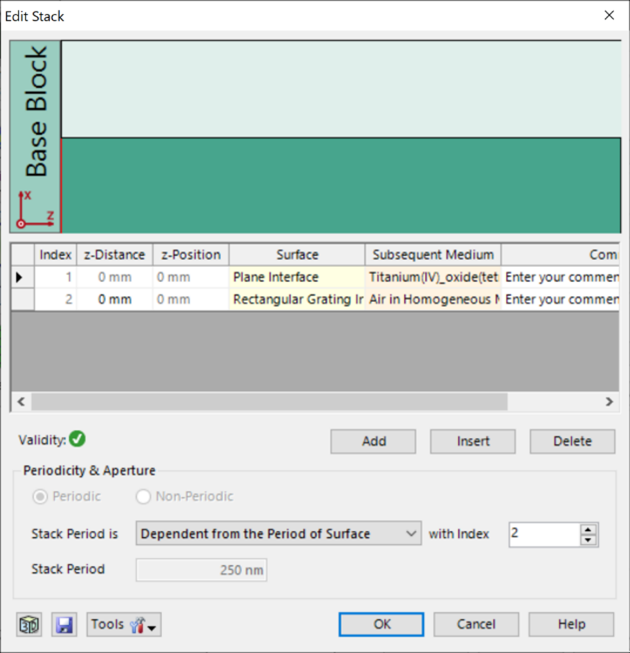 oa1����&9� R�S�zp-sKB 偏振态分析 �|0A n|�18 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 oKzV!~{0M; 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 UyT�q(7uo 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 7q$9\��RR5 /8J2,8vZ� oa1����&9� R�S�zp-sKB 偏振态分析 �|0A n|�18 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 oKzV!~{0M; 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 UyT�q(7uo 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 7q$9\��RR5 /8J2,8vZ� 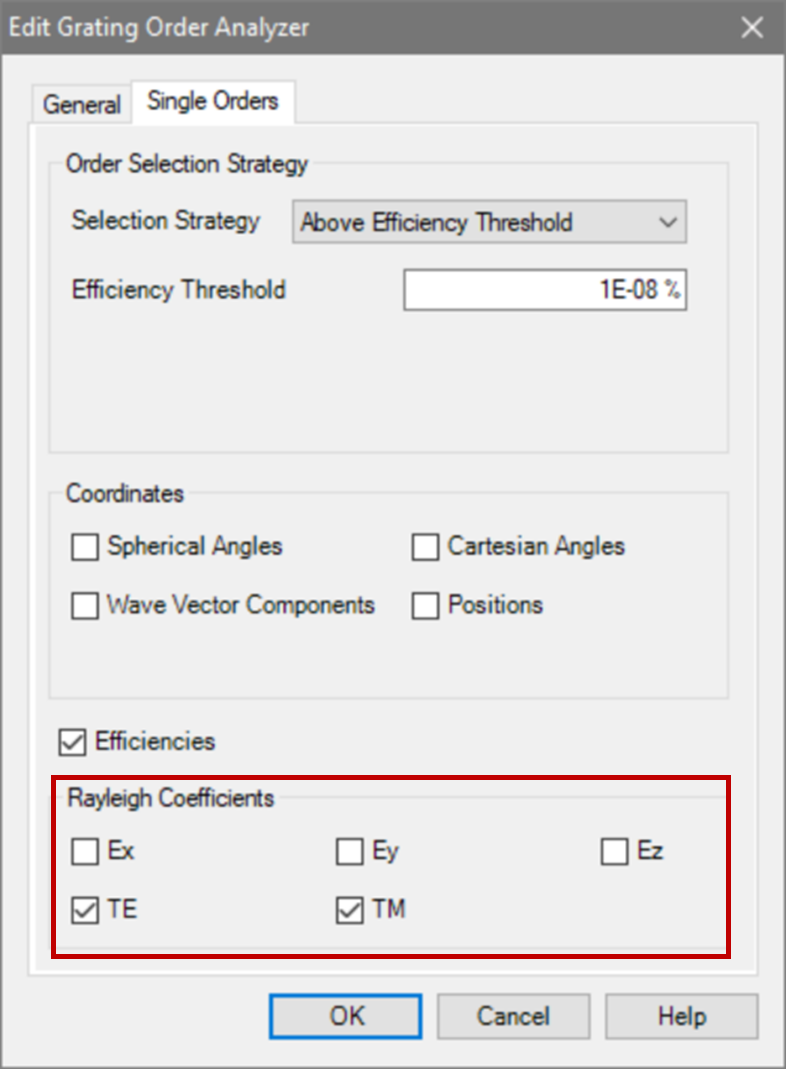 z[����IG+2 'H�Pw�5 �L 模拟光栅的偏振态 i���Tq�v= z[����IG+2 'H�Pw�5 �L 模拟光栅的偏振态 i���Tq�v=
�LP�#CA^*S
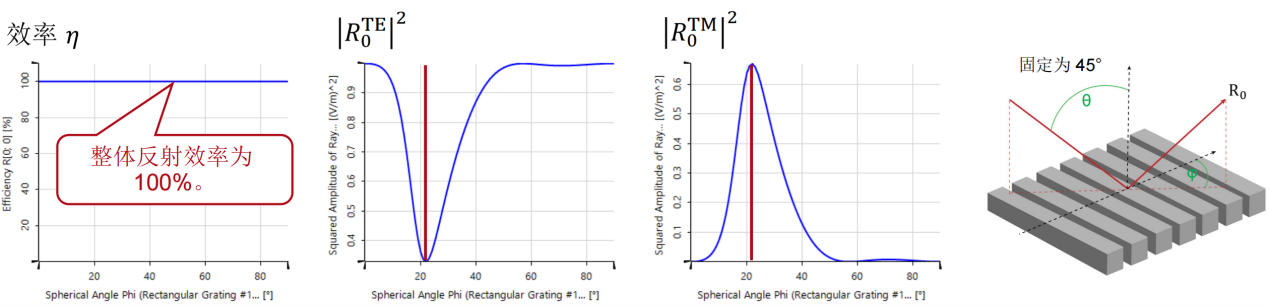 �
���p^\>{ pl|<���g�9 瑞利系数现在提供了偏振态的信息: Z*���j�hSy 在圆锥入射角为0(𝜑=0)时, �
���p^\>{ pl|<���g�9 瑞利系数现在提供了偏振态的信息: Z*���j�hSy 在圆锥入射角为0(𝜑=0)时,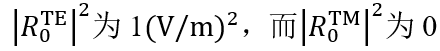 。这说明衍射光是完全偏振的。 lr�,hF1r&Y 对于𝜑=22°, 。这说明衍射光是完全偏振的。 lr�,hF1r&Y 对于𝜑=22°,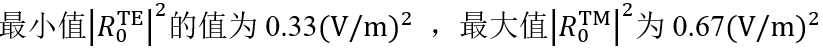 。此时,67%的光是TM偏振的。 D;d�'s�s�; 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 �t�AbIT;�> [sAC��Pn$f Passilly等人更深入的光栅案例。 �~'v^�_�_8 Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 @b-?K��H�� 因此,他们将模拟结果与制作样品的测量数据进行了比较。 ���S#2�'Jw 。此时,67%的光是TM偏振的。 D;d�'s�s�; 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 �t�AbIT;�> [sAC��Pn$f Passilly等人更深入的光栅案例。 �~'v^�_�_8 Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 @b-?K��H�� 因此,他们将模拟结果与制作样品的测量数据进行了比较。 ���S#2�'Jw
�klv^��310
 !OC?3W:^_� �DC�P���"� 光栅结构参数 t�H17��Z�� 在本文中,研究了两种不同的制备光栅结构。 q'"�,70"�\ 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 �8B���o'0
由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 �r$��G�;^� 但是如果有可用数据,就可以详细分析光栅的复杂形状。 @fbvu_�-]. !OC?3W:^_� �DC�P���"� 光栅结构参数 t�H17��Z�� 在本文中,研究了两种不同的制备光栅结构。 q'"�,70"�\ 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 �8B���o'0
由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 �r$��G�;^� 但是如果有可用数据,就可以详细分析光栅的复杂形状。 @fbvu_�-].
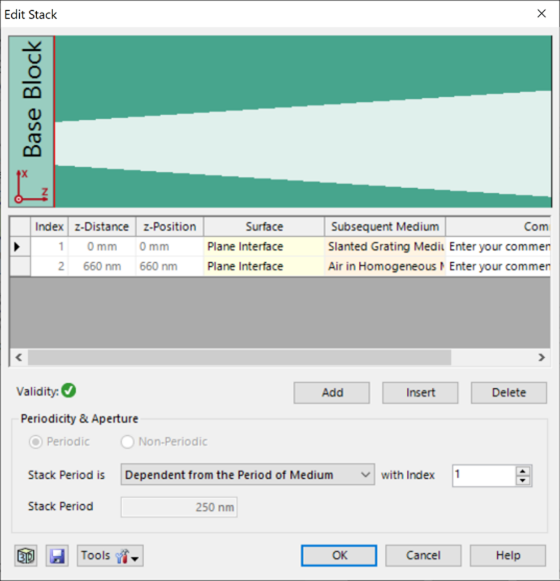
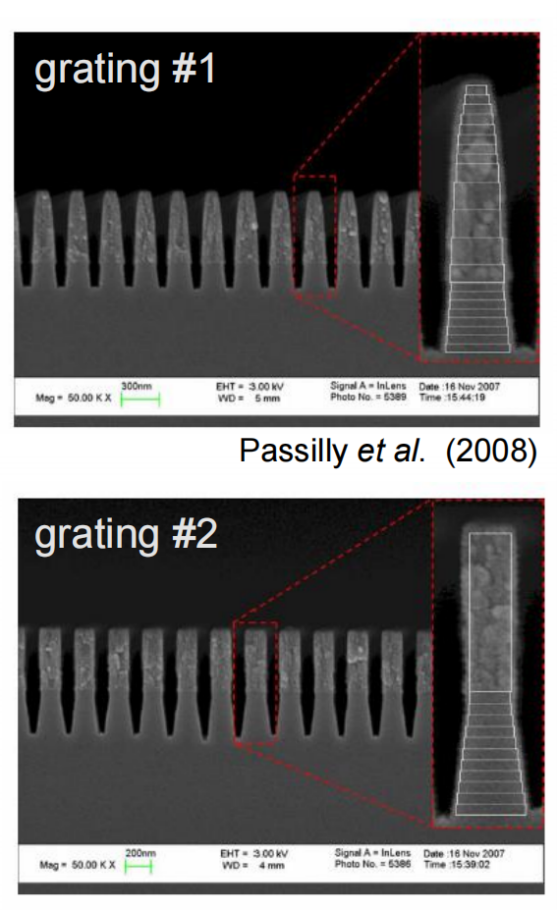 n�b(#;3�DQ x\�I9J�4Q� 光栅#1——参数 q\d'}:k�fu 假设侧壁倾斜为线性。 �oV�,>u5:B 忽略了衬底中的欠刻蚀部分。 pd>EUdbrp& 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 h#;f�BQ]
� 光栅周期:250 nm �n3~xiQ'�� 光栅高度:660 nm ~A>3k2�N/e 填充因子:0.75(底部) �~wh8)r��m 侧壁角度:±6° ~�c�U,3��g n_1:1.46 Gd:f�Wz(�� n_2:2.08 �/��`:5#�O n�b(#;3�DQ x\�I9J�4Q� 光栅#1——参数 q\d'}:k�fu 假设侧壁倾斜为线性。 �oV�,>u5:B 忽略了衬底中的欠刻蚀部分。 pd>EUdbrp& 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 h#;f�BQ]
� 光栅周期:250 nm �n3~xiQ'�� 光栅高度:660 nm ~A>3k2�N/e 填充因子:0.75(底部) �~wh8)r��m 侧壁角度:±6° ~�c�U,3��g n_1:1.46 Gd:f�Wz(�� n_2:2.08 �/��`:5#�O
�F RS@�-P
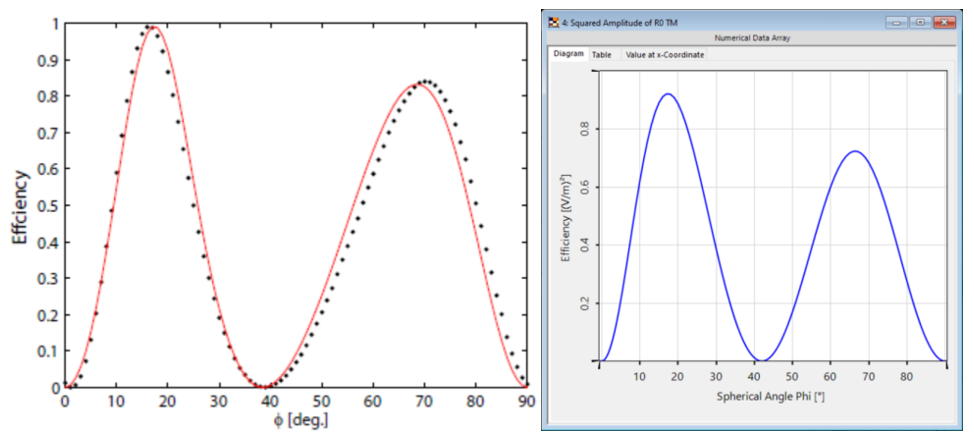
 ��k�<8�:� #H�M0s~^w& 光栅#1——结果 9~Q�.�[� A 这两幅图对比之下匹配度很高,特别是图表的趋势。 qhL�e�[�[> 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 �EDL<J1%�� ,i�,f�1XJ| ��k�<8�:� #H�M0s~^w& 光栅#1——结果 9~Q�.�[� A 这两幅图对比之下匹配度很高,特别是图表的趋势。 qhL�e�[�[> 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 �EDL<J1%�� ,i�,f�1XJ|
 yd`.Rb�&V� e�v�u��@uq 光栅#2——参数 <P��g.���N 假设光栅为矩形。 ��\�HTXl] 忽略了衬底中的欠刻蚀部分。 �G�MB%���A 矩形光栅足以表示这种光栅结构。 CNf���eHMT 光栅周期:250 nm G�)'cd D�1 光栅高度:490 nm �{Qlvj.Xw 填充因子:0.5 HO��&�#Lv� n_1:1.46 W���#��-M| n_2:2.08 ����
�7&l �_2U1$0�xK yd`.Rb�&V� e�v�u��@uq 光栅#2——参数 <P��g.���N 假设光栅为矩形。 ��\�HTXl] 忽略了衬底中的欠刻蚀部分。 �G�MB%���A 矩形光栅足以表示这种光栅结构。 CNf���eHMT 光栅周期:250 nm G�)'cd D�1 光栅高度:490 nm �{Qlvj.Xw 填充因子:0.5 HO��&�#Lv� n_1:1.46 W���#��-M| n_2:2.08 ����
�7&l �_2U1$0�xK 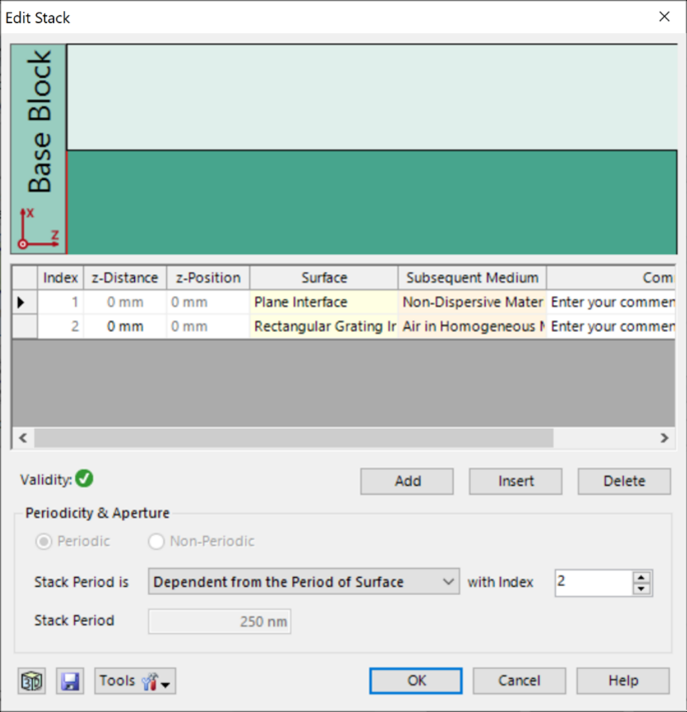 �GJ{�]}�fl �]#+fQR$�! 光栅#2——结果 ]U'�K�Yrh 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 1�w1(FpQO. 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 oy/#,R_�n% �l�,,5OZ�w �GJ{�]}�fl �]#+fQR$�! 光栅#2——结果 ]U'�K�Yrh 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 1�w1(FpQO. 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 oy/#,R_�n% �l�,,5OZ�w 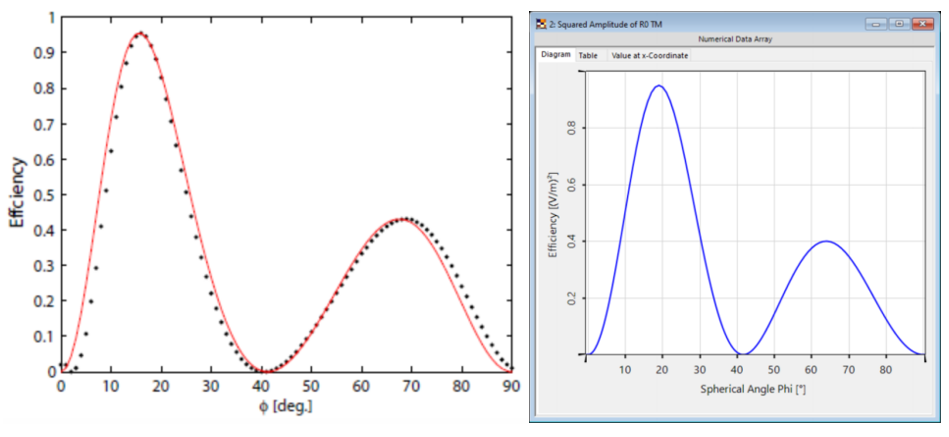 U2@?!B[\d` U2@?!B[\d`
|