-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-11-17
- 在线时间1888小时
-
-
访问TA的空间加好友用道具

|
摘要 �����U6p�G
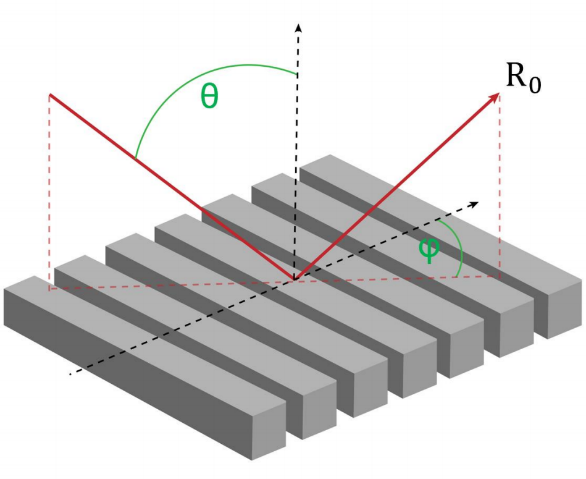
>J \}�&!8, 光栅结构广泛应用于各种光学应用场景,如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM,也称为RCWA),为任意光栅结构的严格分析提供了通用和方便的工具。为此,复杂的一维或二维周期结构可以使用界面和调制介质进行配置,这允许任何类型的光栅形貌进行自由的配置。在此用例中,详细讨论了衍射级次的偏振态的研究。 -zq_W+�)ks i8tH0w/(M�
 �cS�'|c0�6 F^�v <z�)x 任务说明 7|"gMw���/ >c~�F�g�s� �cS�'|c0�6 F^�v <z�)x 任务说明 7|"gMw���/ >c~�F�g�s� 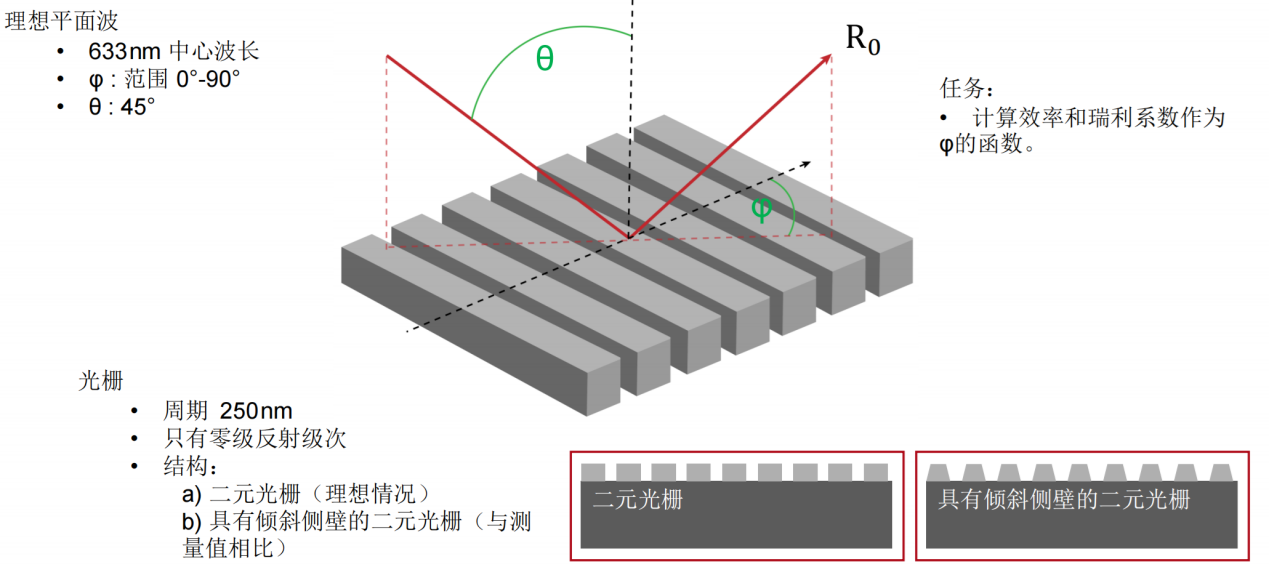 ��1P'R-�I� Wn9b�</�tf 简要介绍衍射效率与偏振理论 ��BpGK`0H� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 �SRix�T+E 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: {bS�i3�o�I ��1P'R-�I� Wn9b�</�tf 简要介绍衍射效率与偏振理论 ��BpGK`0H� 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 �SRix�T+E 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: {bS�i3�o�I 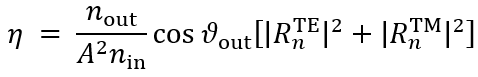 t&�r-;sH^[ 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 �W+'|zh�n� 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: �Z|�z+[V}[ t&�r-;sH^[ 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 �W+'|zh�n� 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: �Z|�z+[V}[ 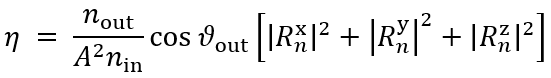 3+%c*�}KC~ 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为 3+%c*�}KC~ 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为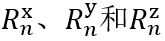 。 .!\�N��M&E �jM E==)Y 。 .!\�N��M&E �jM E==)Y
光栅结构参数 �tW�Nz:�V 研究了一种矩形光栅结构。 M��]��+FTz 为了简化设置,选择光栅配置,只允许零阶(R_0)反射传播。 t/=�x�Y'�7 根据上述参数选择以下光栅参数: %Q}T9%M�tj 光栅周期:250 nm 5F�8sigr/h 填充因子:0.5 �R9/�(z\'} 光栅高度:200 nm azj:Hru&t# 材料n_1:熔融石英(来自目录) 1w)#BYc�=L 材料n_2:二氧化钛(来自目录) �p.gaw16}> Q�zwA*�\�G 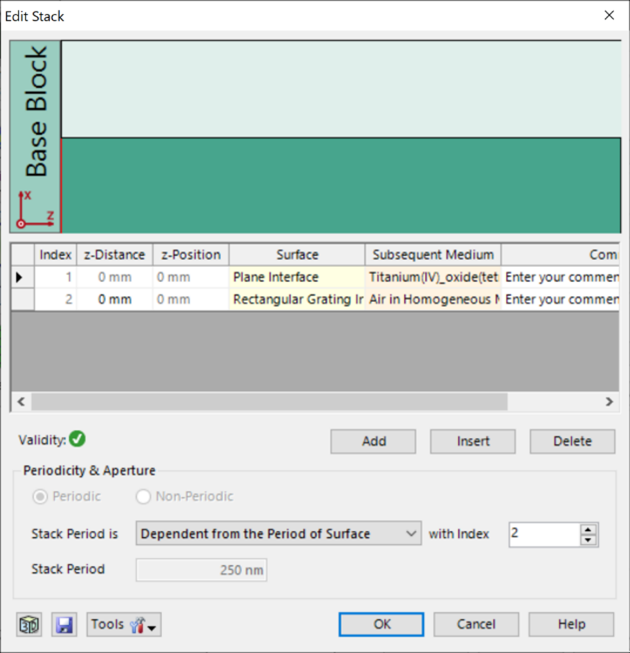 �=]OG5b_-Y P��(1�bd"Q 偏振态分析 *u�Llf'qU] 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 v\Y362X�v� 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 w2��!�5Cb2 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 *o/���Q#� �pN�[G��?A �=]OG5b_-Y P��(1�bd"Q 偏振态分析 *u�Llf'qU] 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 v\Y362X�v� 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 w2��!�5Cb2 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 *o/���Q#� �pN�[G��?A 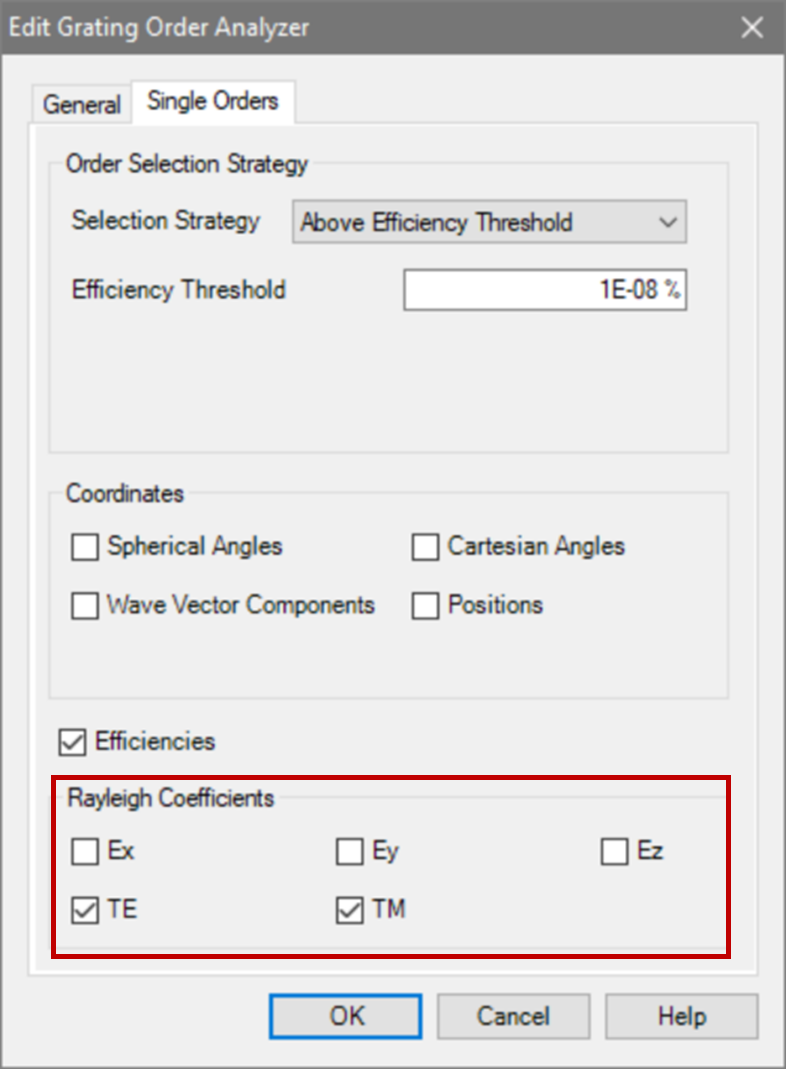 ���)V}u�}5 �fR��=B/`� 模拟光栅的偏振态 }NQ�{S3J�W ���)V}u�}5 �fR��=B/`� 模拟光栅的偏振态 }NQ�{S3J�W
i�#@3\&{J>
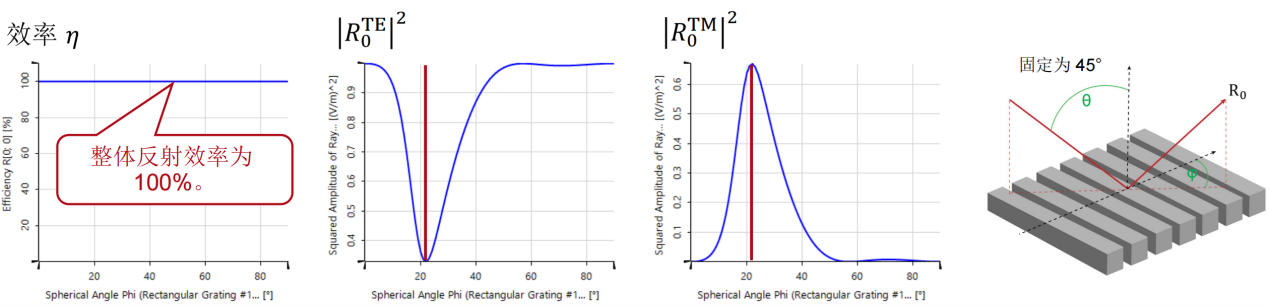 |kHPk)�}I] 8T��K&i�,� 瑞利系数现在提供了偏振态的信息: Yx�a�l�%�� 在圆锥入射角为0(𝜑=0)时, |kHPk)�}I] 8T��K&i�,� 瑞利系数现在提供了偏振态的信息: Yx�a�l�%�� 在圆锥入射角为0(𝜑=0)时,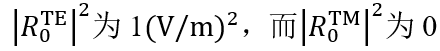 。这说明衍射光是完全偏振的。 �50��:$km\ 对于𝜑=22°, 。这说明衍射光是完全偏振的。 �50��:$km\ 对于𝜑=22°,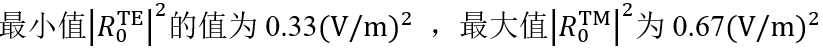 。此时,67%的光是TM偏振的。 ^cE|o&Rm;� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 2Mc}>UI?eO 5z�8!Nmb/ Passilly等人更深入的光栅案例。 =%4vrY
�` Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 "g�)@jqq:> 因此,他们将模拟结果与制作样品的测量数据进行了比较。 xwwy9:ze*l 。此时,67%的光是TM偏振的。 ^cE|o&Rm;� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 2Mc}>UI?eO 5z�8!Nmb/ Passilly等人更深入的光栅案例。 =%4vrY
�` Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 "g�)@jqq:> 因此,他们将模拟结果与制作样品的测量数据进行了比较。 xwwy9:ze*l
+��v 9@du
 yW&|�ZJ�F? �<bPn<QI� 光栅结构参数 26Y�Y1T\B) 在本文中,研究了两种不同的制备光栅结构。 %|l^o�C�+E 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 /
M(A�
kNy 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 <�c[+60�p" 但是如果有可用数据,就可以详细分析光栅的复杂形状。 AwhXCq|�k yW&|�ZJ�F? �<bPn<QI� 光栅结构参数 26Y�Y1T\B) 在本文中,研究了两种不同的制备光栅结构。 %|l^o�C�+E 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 /
M(A�
kNy 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 <�c[+60�p" 但是如果有可用数据,就可以详细分析光栅的复杂形状。 AwhXCq|�k
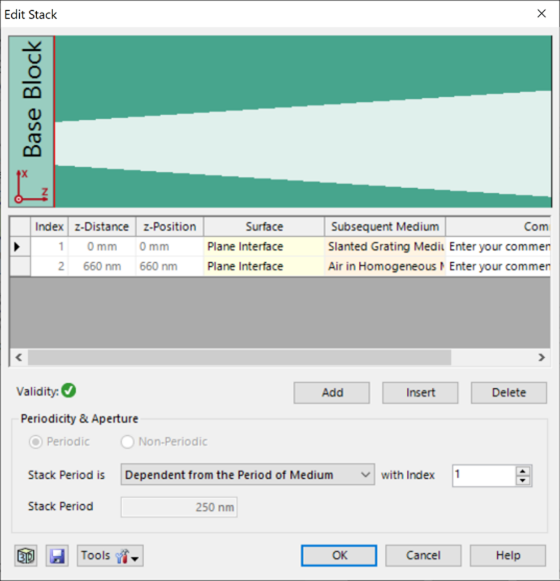
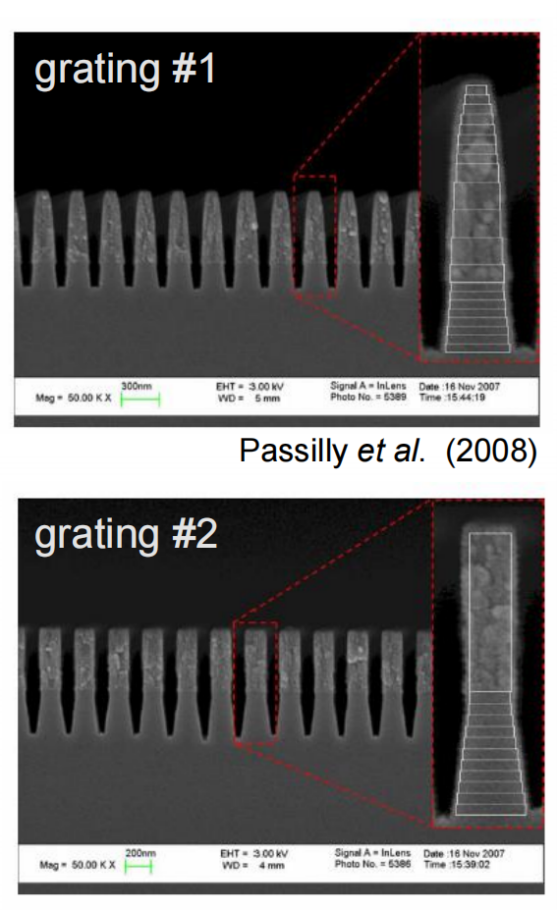 ,cR=W|6cQm MC�Oz-8@|Y 光栅#1——参数 I���/ pv�0 假设侧壁倾斜为线性。 Z|YiYQ�l[) 忽略了衬底中的欠刻蚀部分。 >Lh+(M;�+F 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 : Q�K �)Ym 光栅周期:250 nm $�Ik\^�:�- 光栅高度:660 nm �87P�.K Yy 填充因子:0.75(底部) hw?'aX��K{ 侧壁角度:±6° o(,u"c�/Or n_1:1.46 �=��?U"#a� n_2:2.08 sv<U$M�~)X ,cR=W|6cQm MC�Oz-8@|Y 光栅#1——参数 I���/ pv�0 假设侧壁倾斜为线性。 Z|YiYQ�l[) 忽略了衬底中的欠刻蚀部分。 >Lh+(M;�+F 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 : Q�K �)Ym 光栅周期:250 nm $�Ik\^�:�- 光栅高度:660 nm �87P�.K Yy 填充因子:0.75(底部) hw?'aX��K{ 侧壁角度:±6° o(,u"c�/Or n_1:1.46 �=��?U"#a� n_2:2.08 sv<U$M�~)X
�x[�X�j[�O
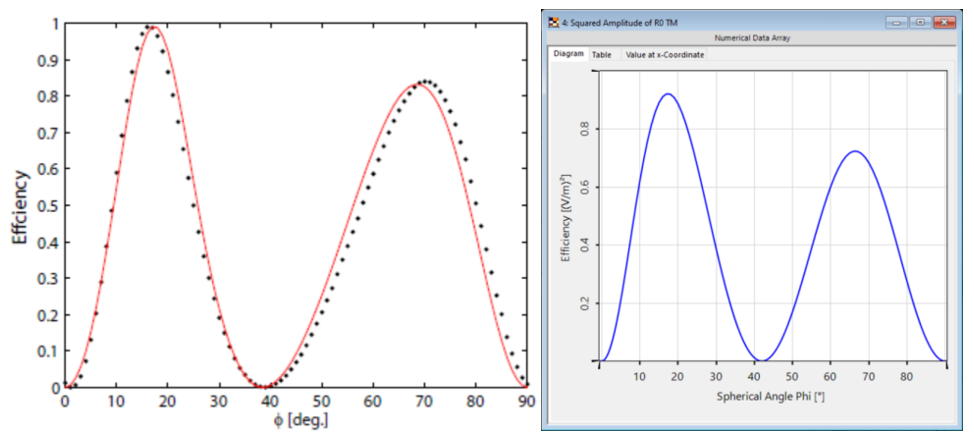
 T@Pt�O��"r \vBpH'hR,' 光栅#1——结果 $z-z�sc�co 这两幅图对比之下匹配度很高,特别是图表的趋势。 �Hq.ys�>�_ 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 =��='~��g~ <$WRc\}&g� T@Pt�O��"r \vBpH'hR,' 光栅#1——结果 $z-z�sc�co 这两幅图对比之下匹配度很高,特别是图表的趋势。 �Hq.ys�>�_ 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 =��='~��g~ <$WRc\}&g�
 {w��Wh��; <lHe��lX=/ 光栅#2——参数 �$a|D����R 假设光栅为矩形。 %K�xL{�HY� 忽略了衬底中的欠刻蚀部分。 �D2$"!7O1H 矩形光栅足以表示这种光栅结构。 ?Q�GA�i�u0 光栅周期:250 nm k T$yHB #� 光栅高度:490 nm BJgg-z�{�Y 填充因子:0.5 M<t>jM@'A# n_1:1.46 n��u�{bEp� n_2:2.08 Pd��c�- �3 w$~|�/UrLf {w��Wh��; <lHe��lX=/ 光栅#2——参数 �$a|D����R 假设光栅为矩形。 %K�xL{�HY� 忽略了衬底中的欠刻蚀部分。 �D2$"!7O1H 矩形光栅足以表示这种光栅结构。 ?Q�GA�i�u0 光栅周期:250 nm k T$yHB #� 光栅高度:490 nm BJgg-z�{�Y 填充因子:0.5 M<t>jM@'A# n_1:1.46 n��u�{bEp� n_2:2.08 Pd��c�- �3 w$~|�/UrLf 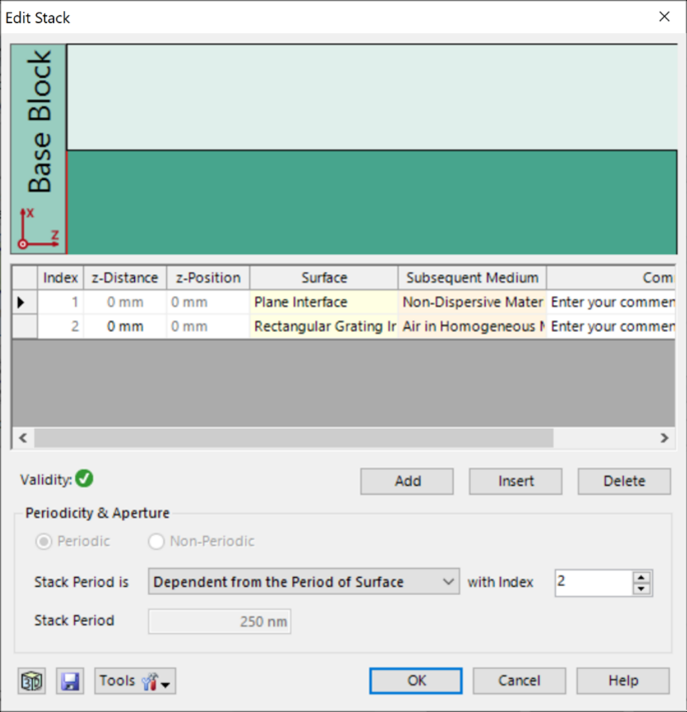 ��-lM4�*+f �>b>���3M' 光栅#2——结果 \`N%7�7��A 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 m�mrx*�sr= 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 a}3sG_(��Y ��"Jw6.q�+ ��-lM4�*+f �>b>���3M' 光栅#2——结果 \`N%7�7��A 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 m�mrx*�sr= 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 a}3sG_(��Y ��"Jw6.q�+ 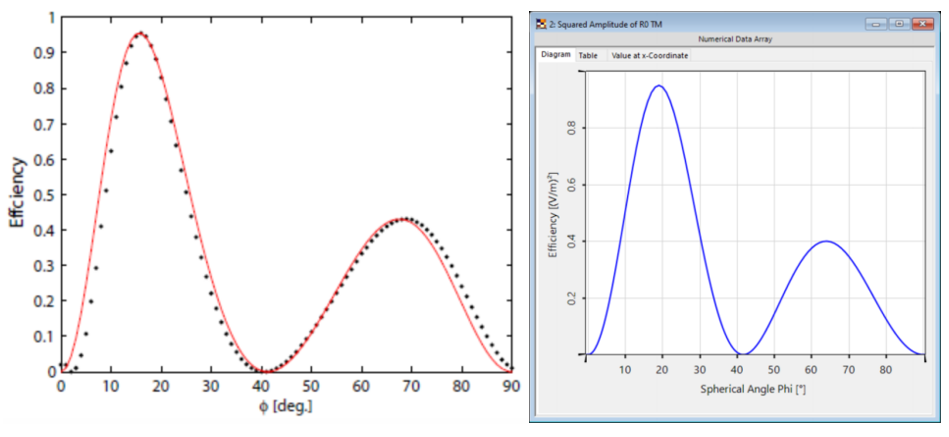 w�(�kN0HD w�(�kN0HD
|