[技术]Savitzky-Golay滤波函数 [复制链接]

1.摘要 `IkWS7|  
`dn|nI2  
在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 id&;

 
因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 =<iK3bPkU  
sh:sPzQ%Jv  
d1``}naNw  
%@kmuz??  
2.如何进入Savitzky-Golay过滤器 e<9IwS!/  
)@\= pE.H  
对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 & 2>W=h  
操作→ jUI'F4.5x-  
杂项→ cZZ-K?_  
Savitzky-Golay过滤器 :=T+sT~  
[[Qu|?KEa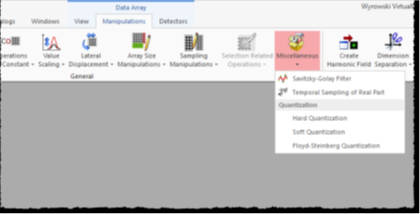  
wC`])z}bT  
^yu0Veypy  
3.可视化的过滤函数 jzdK''CHi  
x<~ pqq8]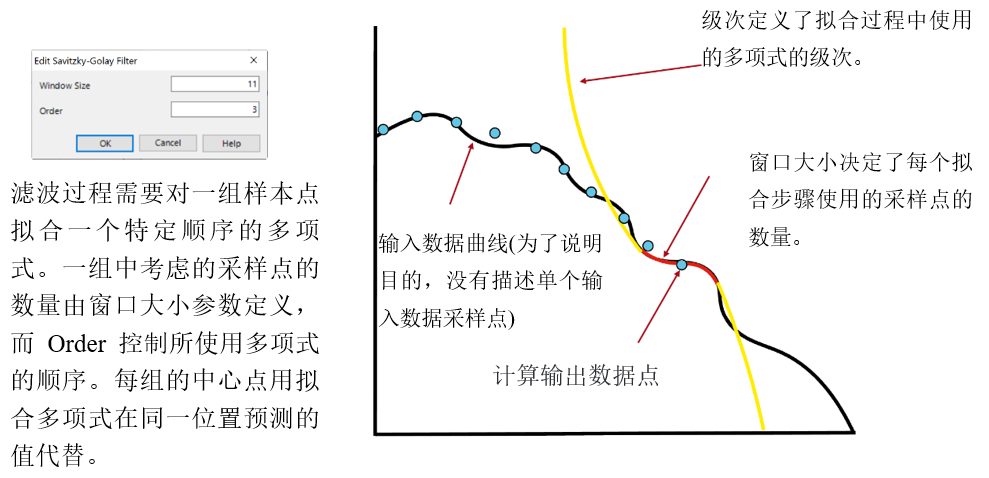  
oh:g  
%W+*)u72(  
4.影响过滤器-窗口大小 @iS(P u  
yFH)PQ_  
更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 EUu"H` E+  
arrNx|y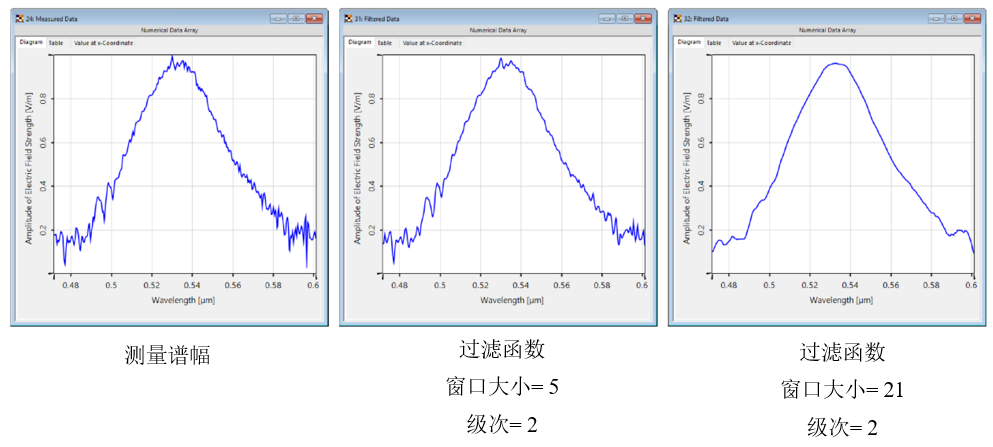  
a~9U{)@F  
3!,XR\`[  
更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 &^{HD }/{b  
&LwR9\sh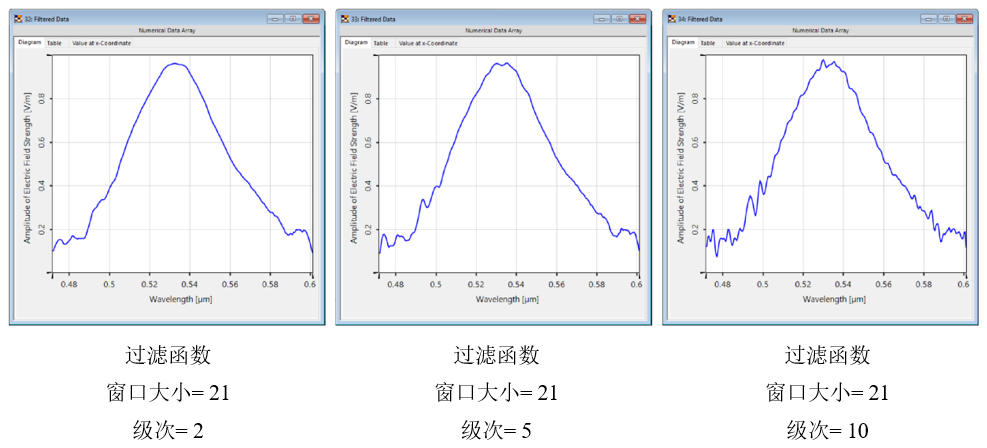  
2}/Z.)^Q  
0}PW<lU-  
5.局部噪声过滤 GTeFDm;T^  
M0S}-eXc5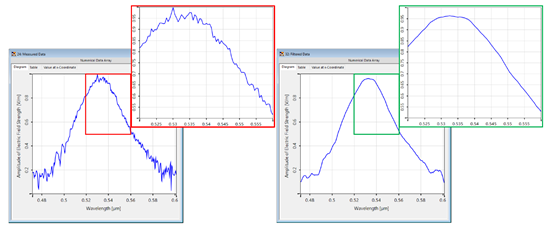  
tl (2=\  
4T{+R{_Y1  
6.FWHM 检测 [C,<Q  
i"r&CS)sT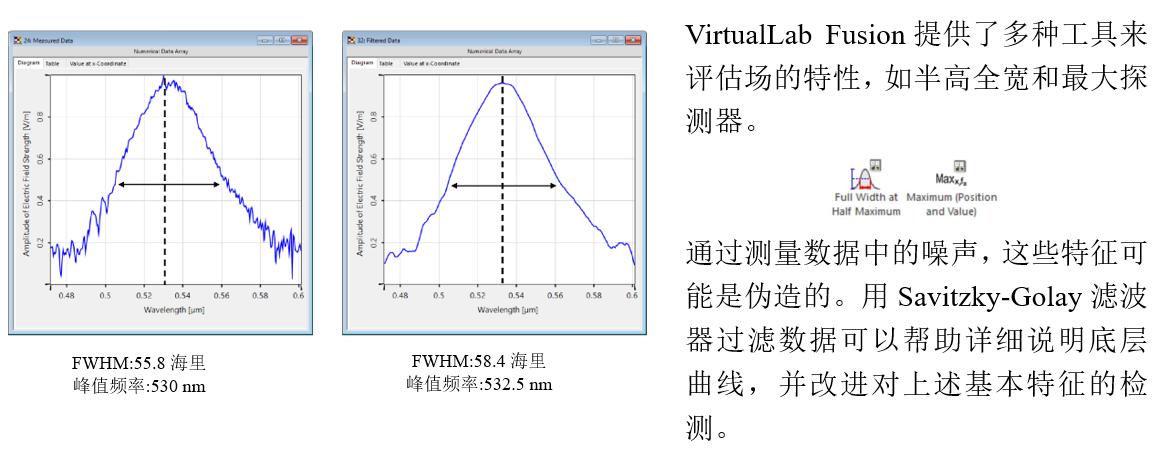  
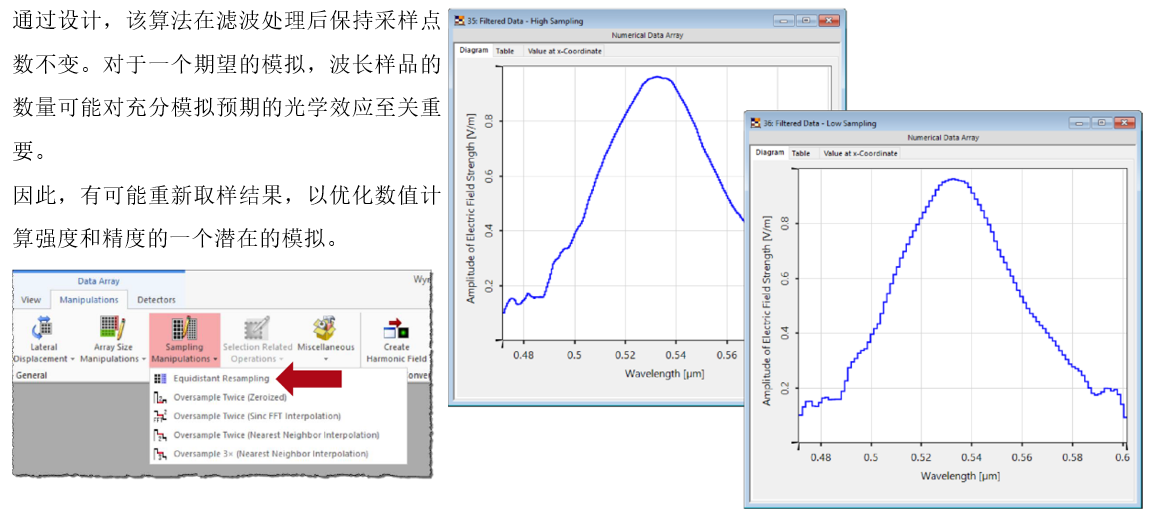
Zq}w}v  
$[by)  
7.等距的重采样 xw&[ 9}Y  
-shS?kV