[技术]Savitzky-Golay滤波函数 [复制链接]

1.摘要 EpW89X  

m~I@q [  
在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 + *W%4e  
因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 po! [Nd&"  
/4I9Elr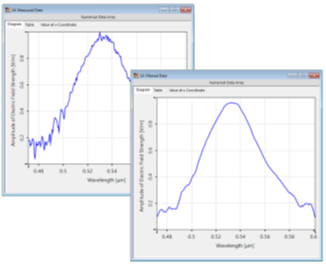  
iFOa9!_0n  
(^
HU|   
2.如何进入Savitzky-Golay过滤器 8l>7=~Egp  
lRANXM  
对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 $6l^::U  
操作→ l5T0x=y9!  
杂项→ \b
;z$P\+*  
Savitzky-Golay过滤器 SgWLs%B  
$jg~a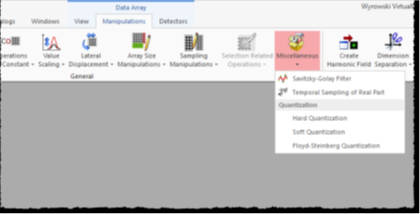  
Fy*t[>  
!59,<N1Iu  
3.可视化的过滤函数 'WNq/z"X  
< ZG!w^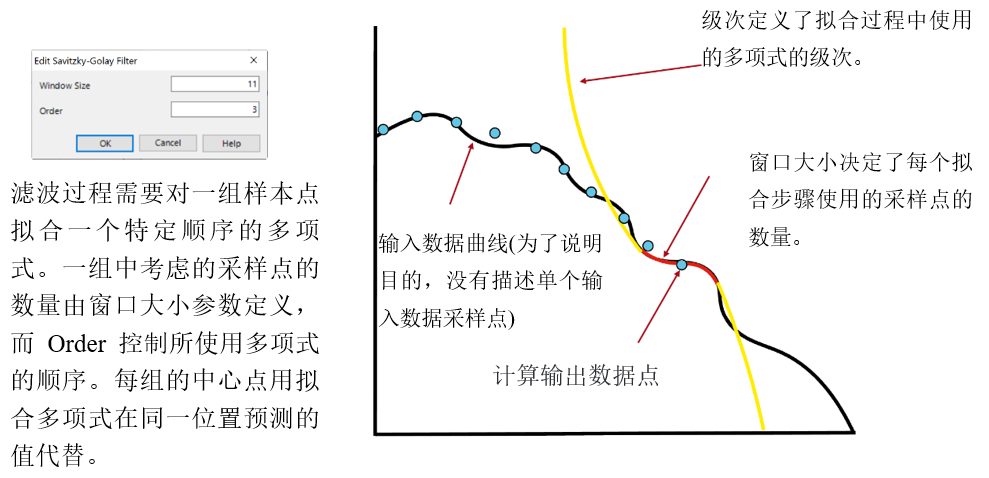  
{
,=U]^A  
<lZVEg  
4.影响过滤器-窗口大小 *x/H   
j.yh>"de  
更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 _oHxpeM  
@rv)J[7Y&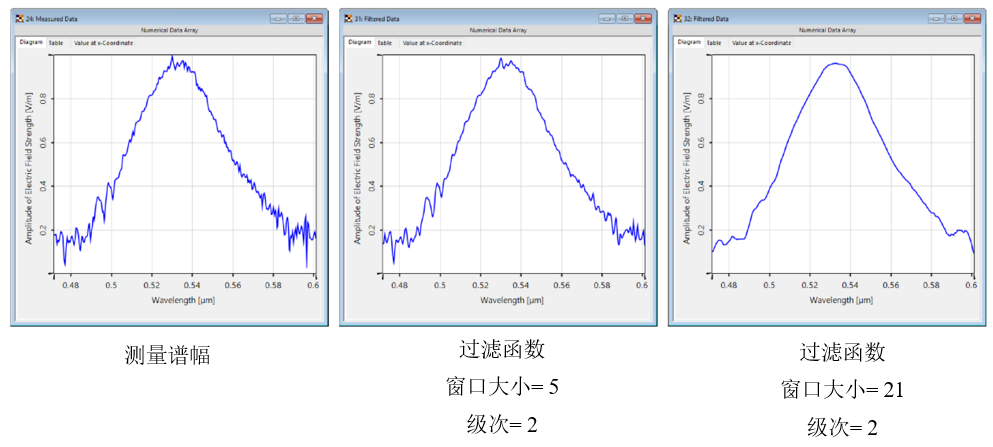  
12V-EG i  
$WiUoS  
更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 |&MOus#v  
z:8ieJ)C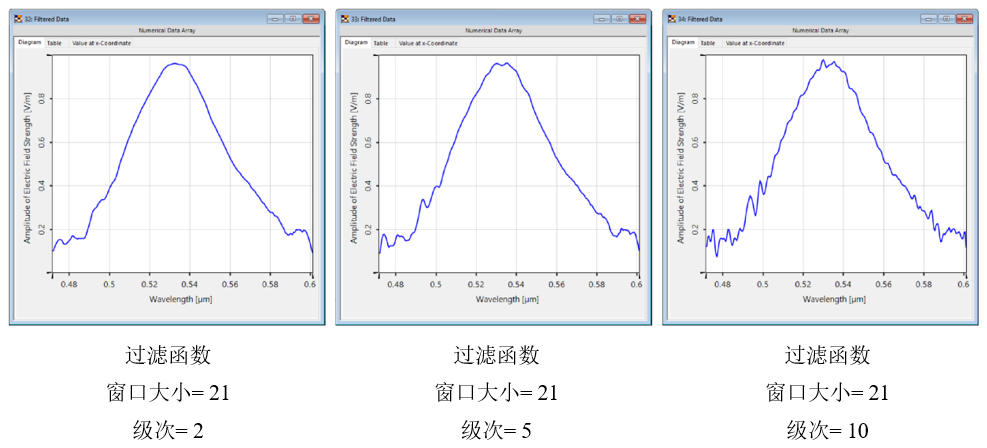  
#h#_xh'  
n0FzDQt26  
5.局部噪声过滤 Elt"tJ  
dG!)<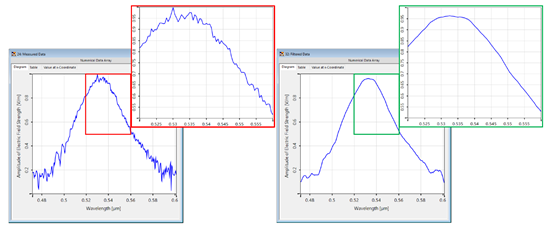  
,:{+-v(  
Us\Nmso z  
6.FWHM 检测 _ mgu r  
*Oq&g\K)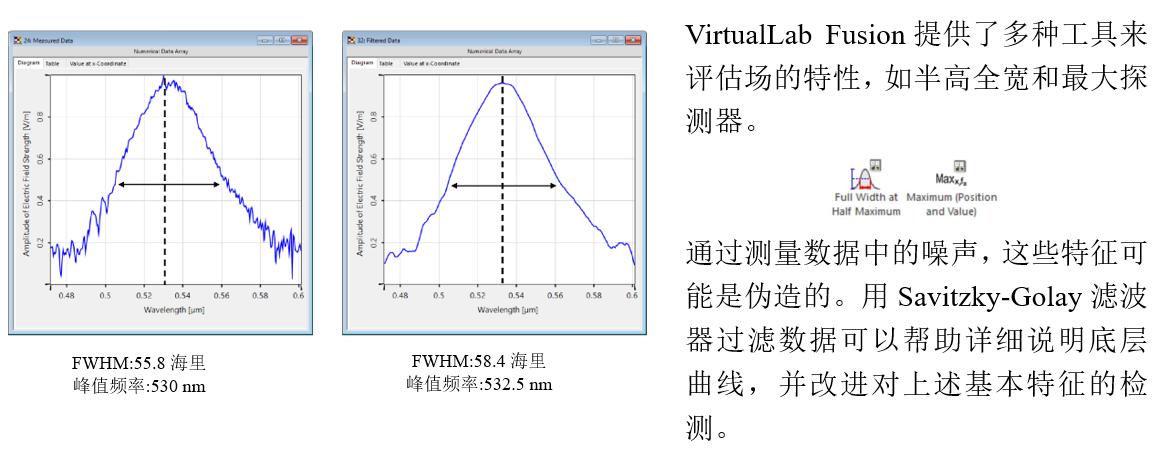  
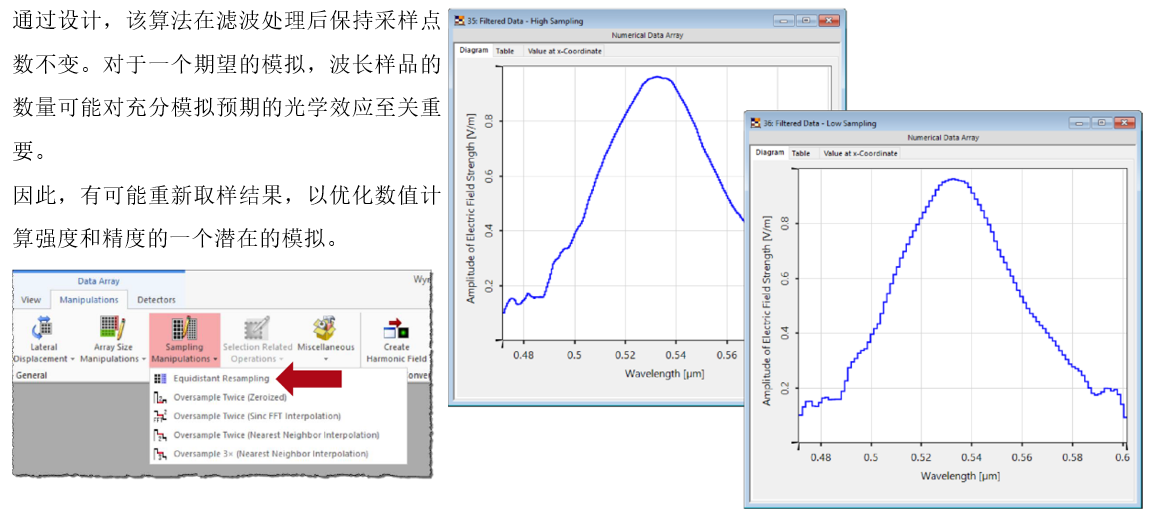
q>6RO2,  
,ZZ5A;)  
7.等距的重采样 iX6*OEl/Q  
<OrQbrWQa