[技术]Savitzky-Golay滤波函数 [复制链接]

1.摘要 `#3FvP@&  
BM>'w,$KL  
在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 ""W*) rR   
因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 f&
2f8@  
@b3jO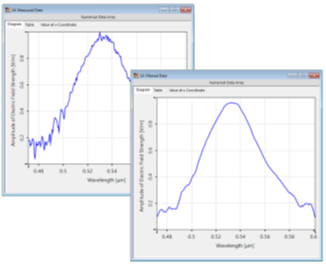  
_`~\zzUZ  
WNO!6*+  
2.如何进入Savitzky-Golay过滤器 0`Hr(J`

F  
yt[vd8O'c  
对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 :vXlni7N[M  
操作→ +t7n6  
杂项→ p0sq{d~  
Savitzky-Golay过滤器 h%PbM`:}6  
231,v,X[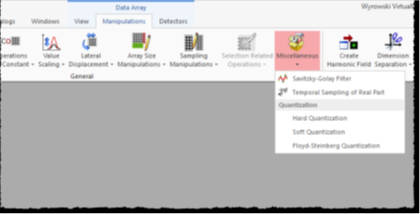  
^~DDl$NH  
> }fw7X  
3.可视化的过滤函数 0nsjihw  
DFM~jlH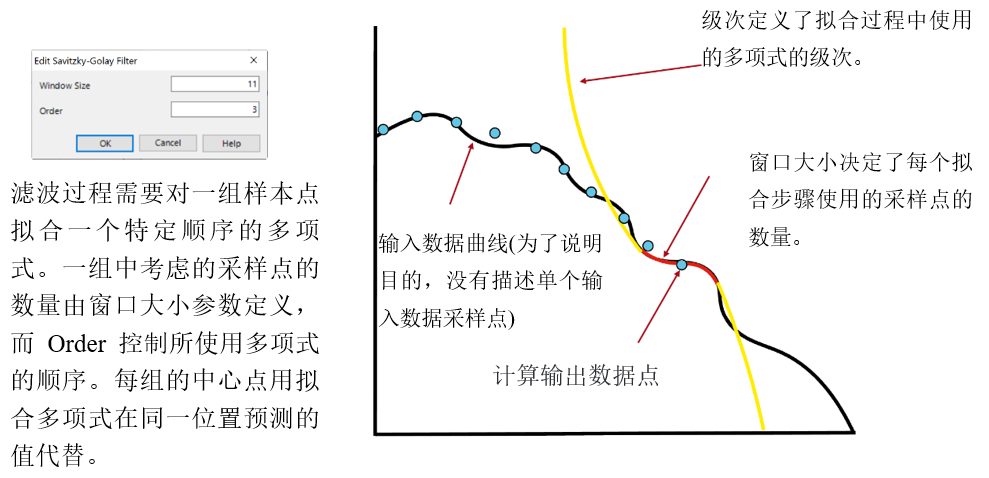  
;6655C  
:cA%lKg  
4.影响过滤器-窗口大小 xe@11/F  
)WH;G:
$&"  
更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 Ql]+,^kA@  
Ba#wW E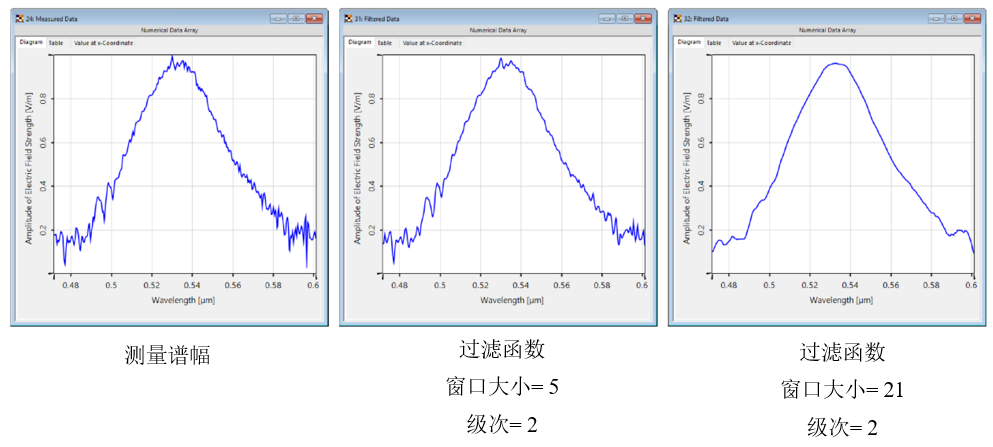  
]9PQKC2&  
$I
|6v  
更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 sLze/D_M*  
rWULv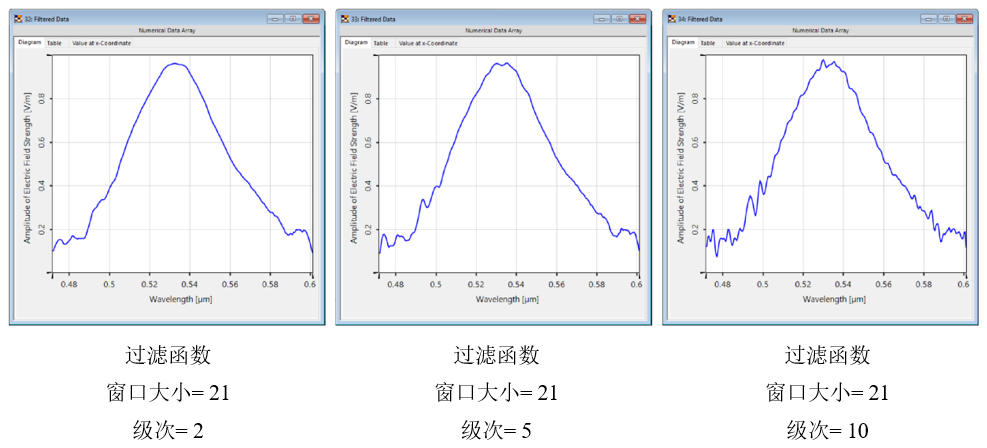  
z,K;GZuP  
yFY:D2  
5.局部噪声过滤 {?RVw`g&f  
j
t`\n1q)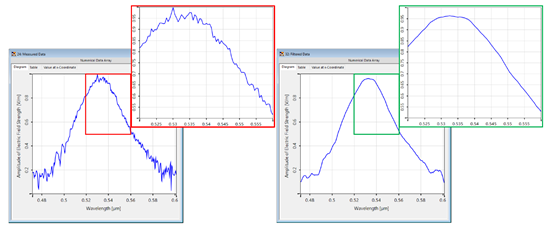  
uA;vW\fHr  
%3Tz%>n  
6.FWHM 检测 I[w;soI  
$!v:@vNMs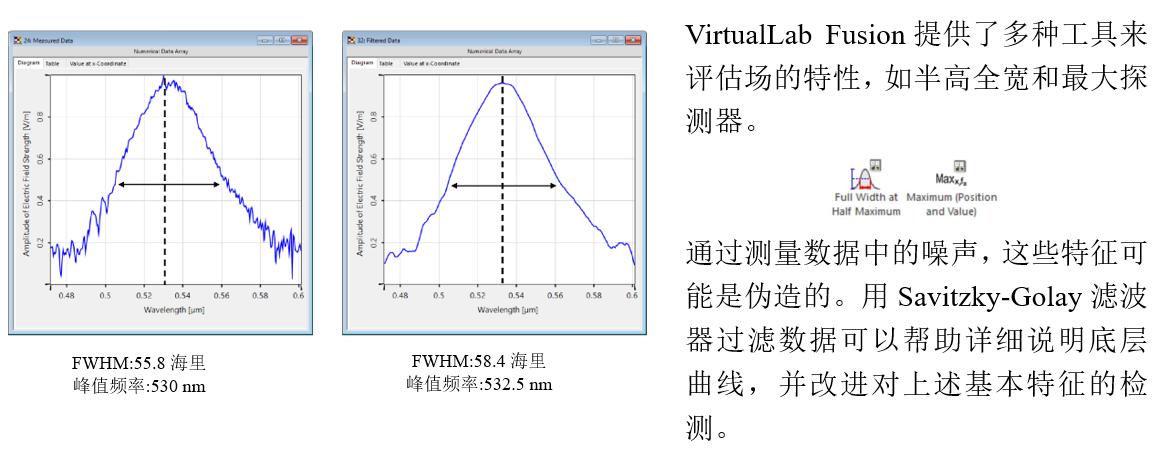  
@Yj+u2!  
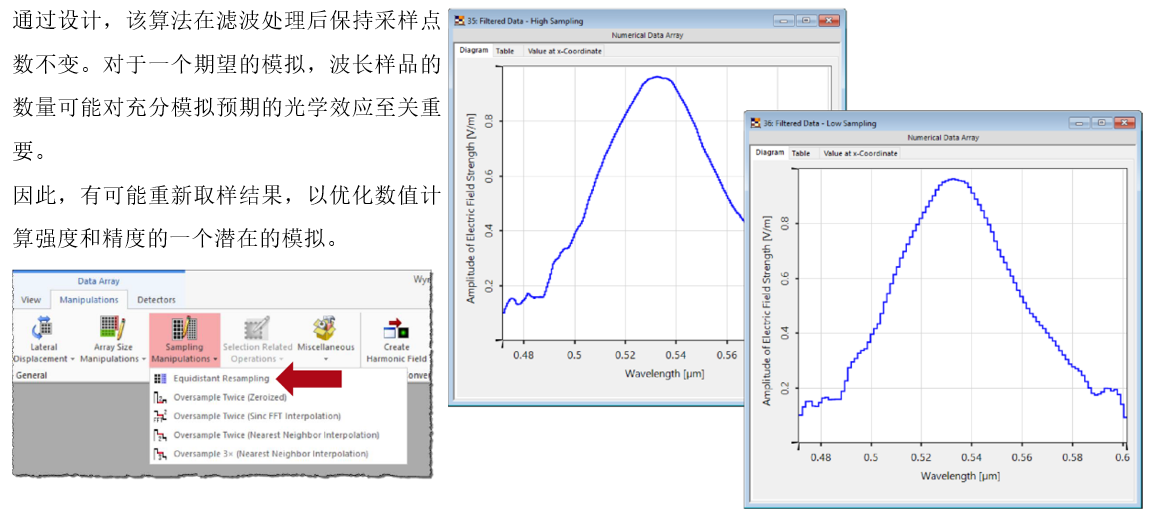
~-2Gx HO`  
7.等距的重采样 h/pm$9A  
kHbH{])