VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
-Z?C�k�!00 >C2HC�6O3  )W9_qmYd"� �e(\Q)re5Q 2. 三种傅里叶变换 k46gY7y,9� =WRO\�lgv. vw
r�RZ"2�
)W9_qmYd"� �e(\Q)re5Q 2. 三种傅里叶变换 k46gY7y,9� =WRO\�lgv. vw
r�RZ"2� 快速傅里叶变换(FFT)
�
�<q�n,�� - 对于不同数值计算,一种
标准而高效的算法。
���^('cbl� 半解析傅里叶变换(SFT)
0!IP�cZjY7 - 一种无需近似的高效重构。
4_<
n�Q9K - 二次相的解析处理,类似chirp-z变换。
���6:R�M�U z_(eQP])�� 逐点傅里叶变换(PSF)
V
[4n'LcE� - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
�k��|ip?�O - 对强波前相位是一种高效而精准的方法。
{�"�4<To]z /W9
�&�Ke� �%AgA -pBp  9UmBm��#"� �X�<K9L7/* 3. 每个元件的设置 ����("F)
&�
>b�+loF :�C��}�H�y
9UmBm��#"� �X�<K9L7/* 3. 每个元件的设置 ����("F)
&�
>b�+loF :�C��}�H�y 傅立叶变换设置
V* Qe5��j9 - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
�1���04!!m - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
�<rMv0y+�r - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
.�WO�/=#�O p�)�z-�W�( 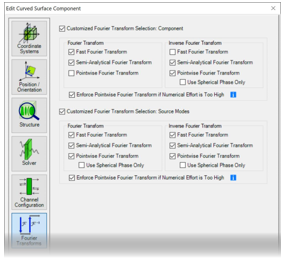 zW)gC9_|m- a8NVLD�>7} 4. 每个元件的设置 @�$���ft�G 5h(jeT�8�"
zW)gC9_|m- a8NVLD�>7} 4. 每个元件的设置 @�$���ft�G 5h(jeT�8�" 傅里叶变换设置
f�n?VNZ`J
_�jD���S"� 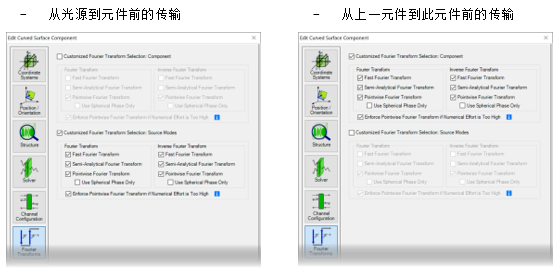 ,7I},sZj�� zg7G^!P��U 5. 默认的傅里叶变换设置 �Q��%M_� � YME[%�c2�x =?+w)(�*0c
,7I},sZj�� zg7G^!P��U 5. 默认的傅里叶变换设置 �Q��%M_� � YME[%�c2�x =?+w)(�*0c
光源模式和探测器的设置
�n\�*�J�aY - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
() <`t}�FQ - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
:B+Rg c�qi �Rd v�n)K� 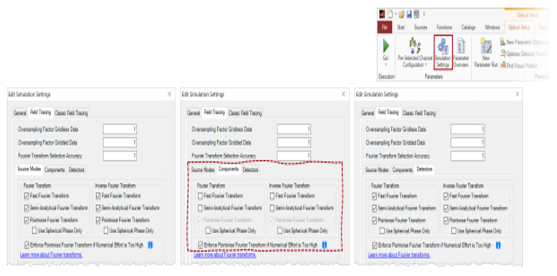 ��sr�4j�Qo yI:r7=��KO 6. 特殊情况 $*i7?S@~-� c�LH�F9B�5 �Dx0O'uwR
��sr�4j�Qo yI:r7=��KO 6. 特殊情况 $*i7?S@~-� c�LH�F9B�5 �Dx0O'uwR 多表面元件
�p�}f�-c�� - 对下列情况应当特别考虑
q�T�S�@D� •透镜系统元件
5�F���r�;� •球面
透镜元件
2J�&XNV^tJ - 此类组件可以理解为
�y�,^";�7U •一组曲面元件,以及
� /+�N�|�X •之间有一些自由空间
B����MY�>a - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
To">��D�Ot Vl4Z_viNH� 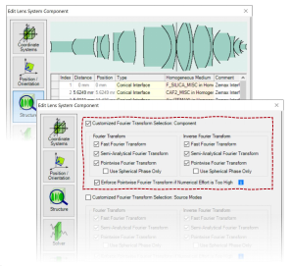 >KKe�V�(Ur v*vn<nPAQ>
>KKe�V�(Ur v*vn<nPAQ> 在k域的元件
#�_{0Nd�p2 - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
�jwq\s�tjD - 这适用于以下情况
�D�QMPAj. •平面表面元件
_2#ze��T5 •分层介质元件
�Jx�n3��$� •光栅元件
A1�=_nt�)5 •功能
光栅元件
%`�eJ66T�� qj`,qm
�P 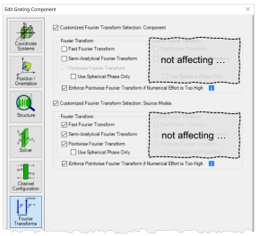 PqVW'�FYe� ��h)^d�B,~ 实例#1:低菲涅尔数系统中的针孔 u�FC?_q?4\ p %L1uwL�G
PqVW'�FYe� ��h)^d�B,~ 实例#1:低菲涅尔数系统中的针孔 u�FC?_q?4\ p %L1uwL�G 1. 实例#1:
成像的光源模式
hR!�}u}ECd ��T0YD�fo�  \WiqN*Z�F� YWS��z�84d �d�i--:h/ 2. 实例#1:系统内部包含的衍射效应 �ka!Bmv��) =w?�M_[&K)
\WiqN*Z�F� YWS��z�84d �d�i--:h/ 2. 实例#1:系统内部包含的衍射效应 �ka!Bmv��) =w?�M_[&K) 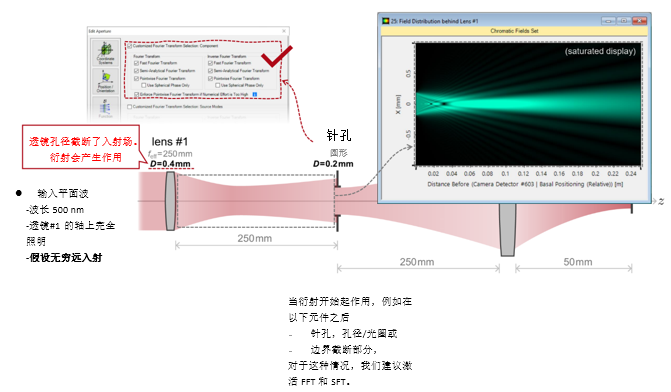 b~j�Iv:9T�
b~j�Iv:9T� 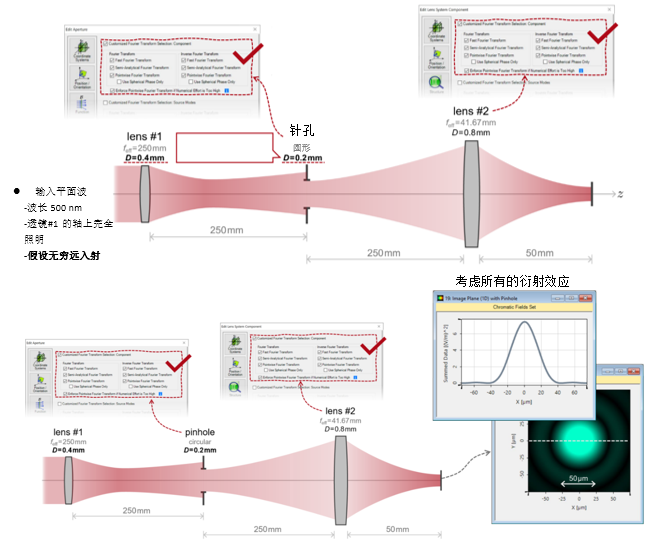 [7'#��~[a~ p�Xve02b1B 3. 实例#1:出瞳衍射法 5dqQws-,?1 7�5kKDR}6�
[7'#��~[a~ p�Xve02b1B 3. 实例#1:出瞳衍射法 5dqQws-,?1 7�5kKDR}6� 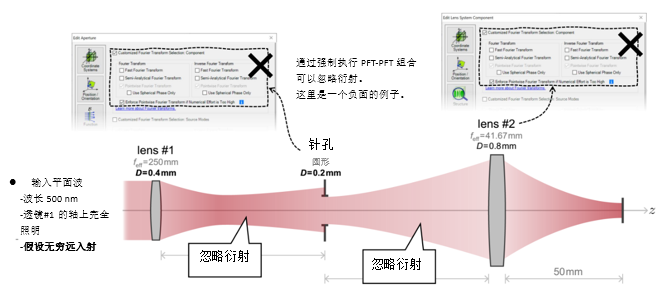 ��o>@=N2�n
��o>@=N2�n 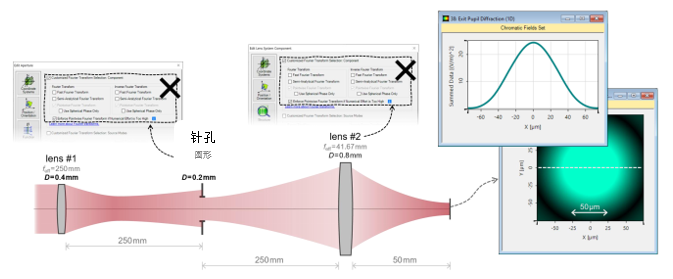 .\U�l!&��y 4. 实例#1:出瞳衍射与对比 R�$Zv�0�a& ��5/��t��j
.\U�l!&��y 4. 实例#1:出瞳衍射与对比 R�$Zv�0�a& ��5/��t��j 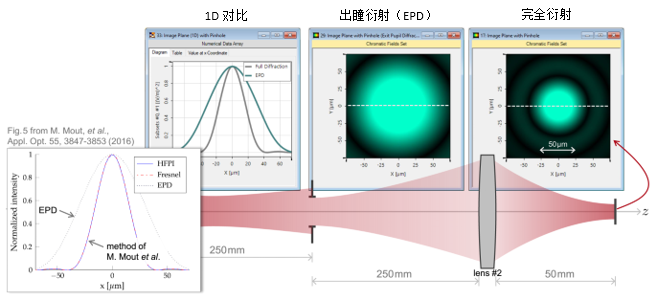 Ze�#J�h�n@ zIP[R):3&U 实例#2:用于激光导星的无焦系统 Cy<T �Vk�8 {�d�^Q7A:` 1. 实例#2:包含所有可能的衍射 �G4O,^ v;Q
Ze�#J�h�n@ zIP[R):3&U 实例#2:用于激光导星的无焦系统 Cy<T �Vk�8 {�d�^Q7A:` 1. 实例#2:包含所有可能的衍射 �G4O,^ v;Q
I�$+��%~4�
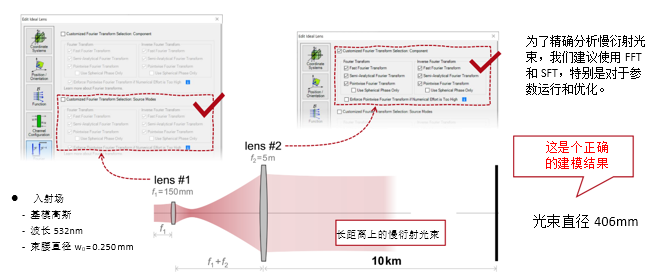 T~�s&)wD��
"Ys�_ �\� ��S|~��i�> 2. 实例#2:忽略透镜间的衍射效应 "�!x�vpsy� "|F.�'qZrm
T~�s&)wD��
"Ys�_ �\� ��S|~��i�> 2. 实例#2:忽略透镜间的衍射效应 "�!x�vpsy� "|F.�'qZrm 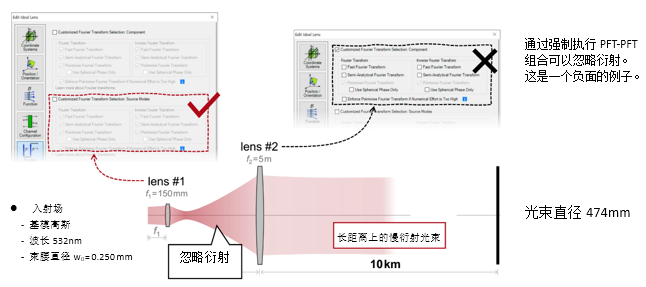 #m[vn^8B]y �o�k%�EqO 实例#3:剪切干涉法的准直测试 ��Tku�/OG' a��nK�[P'Y 1. 例#3:刻意忽略衍射 O��|�?��Z~ �TP~�(
�r�
#m[vn^8B]y �o�k%�EqO 实例#3:剪切干涉法的准直测试 ��Tku�/OG' a��nK�[P'Y 1. 例#3:刻意忽略衍射 O��|�?��Z~ �TP~�(
�r� 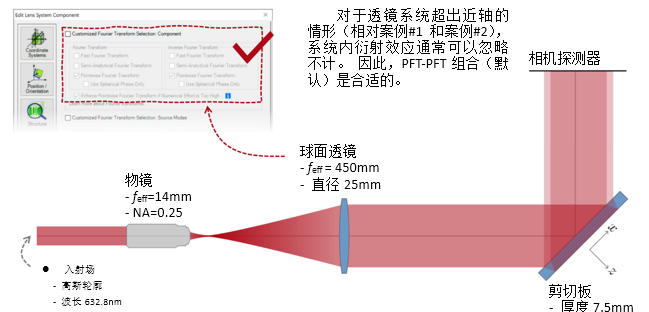 ftO+.-sm<� ?hxK/%�)�� �6
M*�b�6�
ftO+.-sm<� ?hxK/%�)�� �6
M*�b�6�
CKx�\V�+\O
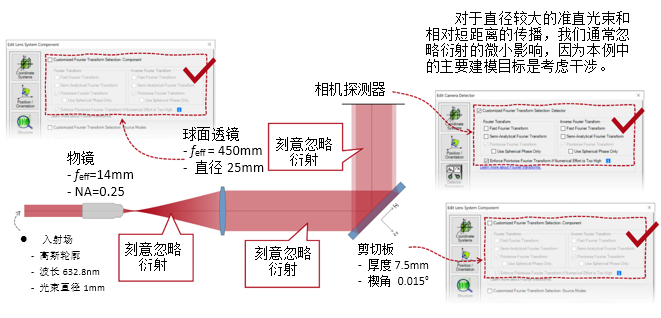 mgo'MW\��
mgo'MW\�� 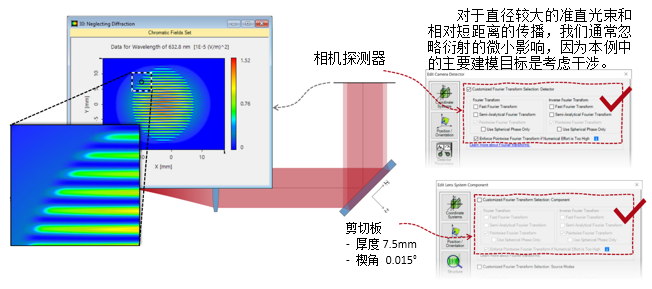 )�!�N2'Ld� 2. 实例#3:包含衍射 �y=��-{�Q� t�ceIA8d6
)�!�N2'Ld� 2. 实例#3:包含衍射 �y=��-{�Q� t�ceIA8d6
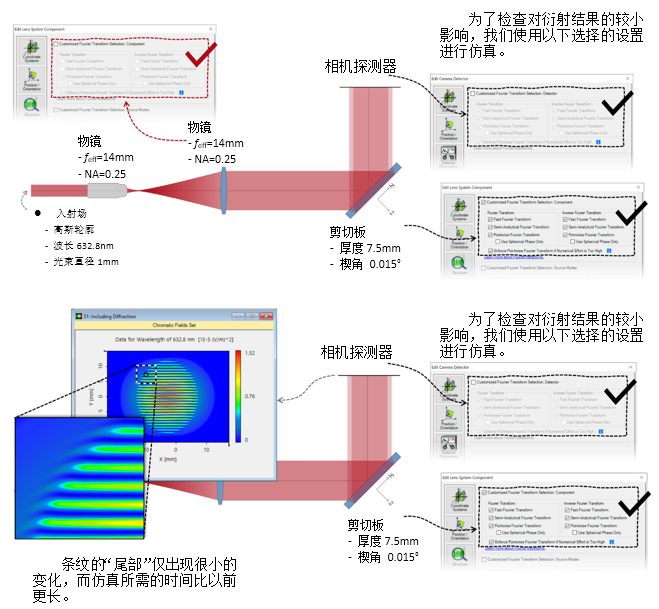 6�lN?)�<uQ
6�lN?)�<uQ