VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
{u�dr�T"�h =M�l�|l��$  V)�2"l"K�t �x
HY+�q�; 2. 三种傅里叶变换 &�@=u+)^-{ jz
%;4e�~t l!\1,J�:}Z
V)�2"l"K�t �x
HY+�q�; 2. 三种傅里叶变换 &�@=u+)^-{ jz
%;4e�~t l!\1,J�:}Z 快速傅里叶变换(FFT)
�`���!z��Q - 对于不同数值计算,一种
标准而高效的算法。
w|&��,I4[" 半解析傅里叶变换(SFT)
B`�LD7]�ew - 一种无需近似的高效重构。
N���V:>�a - 二次相的解析处理,类似chirp-z变换。
�Hv��AE,0N k��VWGDI$~ 逐点傅里叶变换(PSF)
�t �G]N*%@ - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
P\.W��Xe#j - 对强波前相位是一种高效而精准的方法。
~�af8p� {� F\�;2�i:�( ��U%D��it  l<$rq�z3D� �/C��Ix$G� 3. 每个元件的设置 : @s8�?e�g '����^hsH1 )��r=9]�0=
l<$rq�z3D� �/C��Ix$G� 3. 每个元件的设置 : @s8�?e�g '����^hsH1 )��r=9]�0= 傅立叶变换设置
��*�f{�7� - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
{�"�:c��@I - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
M�#`��{>R| - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
TK�K,�Y{{� �]GcV�0&�| 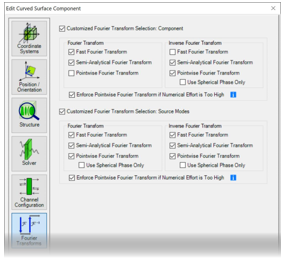 &xgZF�S��q bi+�9�R-=& 4. 每个元件的设置 �C�m^Yl��p Xc{ZN1 �4n
&xgZF�S��q bi+�9�R-=& 4. 每个元件的设置 �C�m^Yl��p Xc{ZN1 �4n 傅里叶变换设置
9`&?hi49nK ol50�d73�B 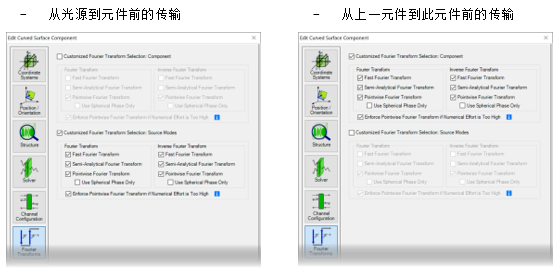 yX��kt:O,i gRHtgR)T�3 5. 默认的傅里叶变换设置 VX�i�ui'/( [9Lxh�P��i �[U��s�wf3
yX��kt:O,i gRHtgR)T�3 5. 默认的傅里叶变换设置 VX�i�ui'/( [9Lxh�P��i �[U��s�wf3
光源模式和探测器的设置
RZ*<n�$�#6 - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
[@�ILc*2O - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
�SBC~QD>L+
�l@xW�Qj9 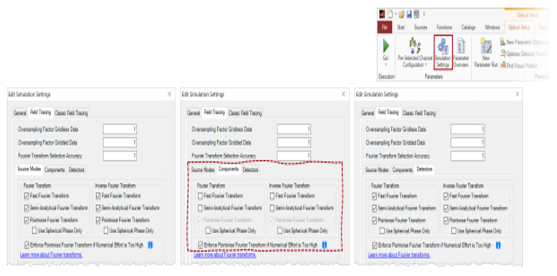 gglf\)E;}E lBS"3s38�4 6. 特殊情况 46ILs1T�6� VD�G|>#[! 3�eWJt\}?B
gglf\)E;}E lBS"3s38�4 6. 特殊情况 46ILs1T�6� VD�G|>#[! 3�eWJt\}?B 多表面元件
�lHcA� j{6 - 对下列情况应当特别考虑
s�u}&�".e^ •透镜系统元件
<o2,HTWNPS •球面
透镜元件
w�"�1�x=+� - 此类组件可以理解为
kY=�r�z&?U •一组曲面元件,以及
P`tyB�e#= •之间有一些自由空间
��|h�c\j�b - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
��0Yp>+:�# �*���-�6? 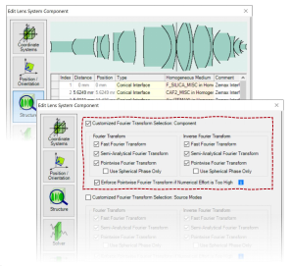 M%3Wy"YQ,n w#sq'v�o4%
M%3Wy"YQ,n w#sq'v�o4% 在k域的元件
+N7"ER�Oc� - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
?HV��}mS[t - 这适用于以下情况
oooS s&t�� •平面表面元件
���)Z("O[� •分层介质元件
]�Y{,N��x� •光栅元件
;�>8kPG��� •功能
光栅元件
��G�y9
$Wj lirN�YJ]tO  ,%k���mXh 5\�xr?`VZ� 实例#1:低菲涅尔数系统中的针孔 EsTB(�9c?� p�c�nl�0o~
,%k���mXh 5\�xr?`VZ� 实例#1:低菲涅尔数系统中的针孔 EsTB(�9c?� p�c�nl�0o~ 1. 实例#1:
成像的光源模式
[z��2eC��H 0iV�;g`�%  �fCg@FHS&^ ��Je 3�1". d+0^u(gc!8 2. 实例#1:系统内部包含的衍射效应 ?,>5[Ha�^? Ch t%�uzb,
�fCg@FHS&^ ��Je 3�1". d+0^u(gc!8 2. 实例#1:系统内部包含的衍射效应 ?,>5[Ha�^? Ch t%�uzb, 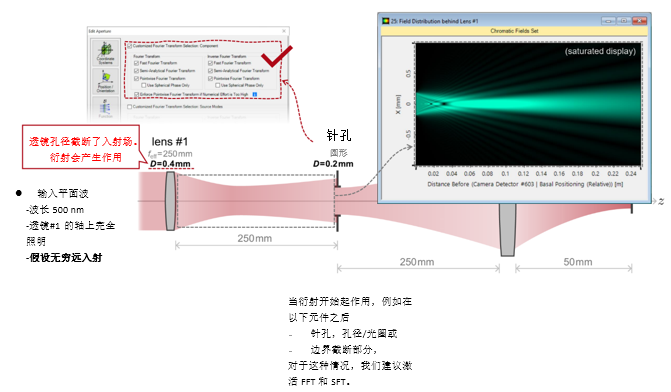 &��s�d�x`,
&��s�d�x`, 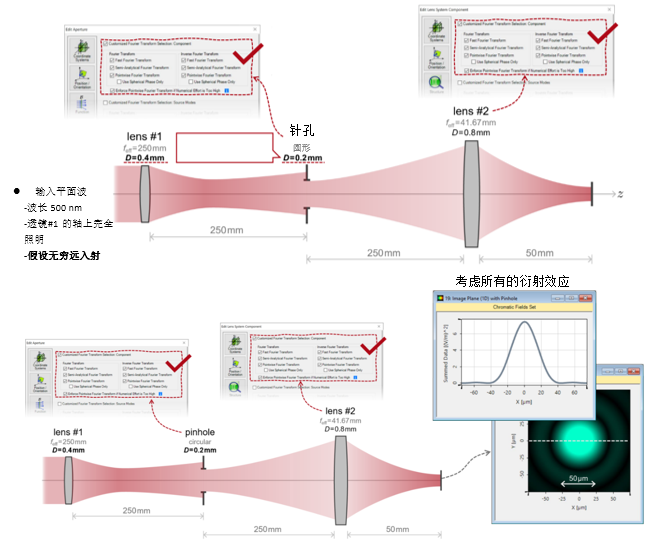 bJwc1AJ�gH y�yjw�?#\8 3. 实例#1:出瞳衍射法 i�y}xI�C�t '$?du�~L-�
bJwc1AJ�gH y�yjw�?#\8 3. 实例#1:出瞳衍射法 i�y}xI�C�t '$?du�~L-� 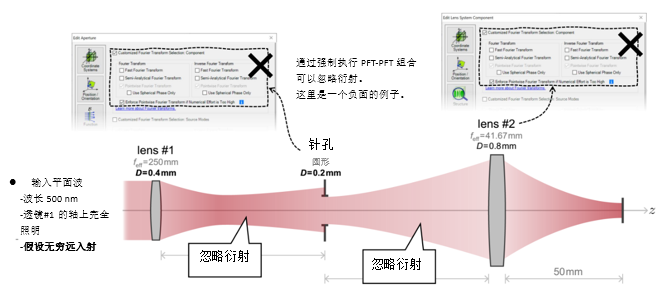 ~;8I5�Sg�e
~;8I5�Sg�e 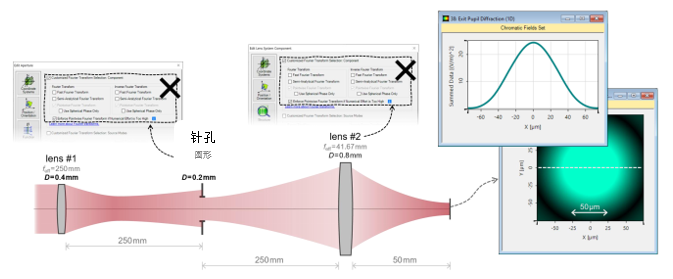 J�0sG�vj{� 4. 实例#1:出瞳衍射与对比 �Wx�n#Rk#> �z+
�Z�G1\
J�0sG�vj{� 4. 实例#1:出瞳衍射与对比 �Wx�n#Rk#> �z+
�Z�G1\ 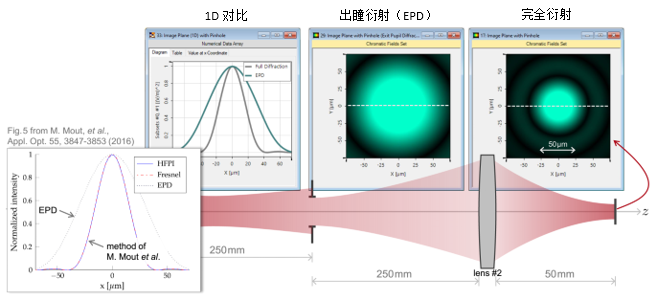 #�3+~�.,X9 p�31o�L�{D 实例#2:用于激光导星的无焦系统 n�+rM"Gx�z !VRo�*[yD@ 1. 实例#2:包含所有可能的衍射 uFo/s�&6K
#�3+~�.,X9 p�31o�L�{D 实例#2:用于激光导星的无焦系统 n�+rM"Gx�z !VRo�*[yD@ 1. 实例#2:包含所有可能的衍射 uFo/s�&6K
C `6S}f��,
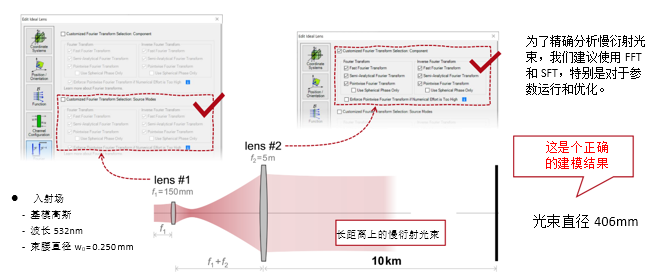 j;��+["mi
��z&F5�mp@ X8��Fzs!L` 2. 实例#2:忽略透镜间的衍射效应 �5{�X��*�a �`;��cz�;"
j;��+["mi
��z&F5�mp@ X8��Fzs!L` 2. 实例#2:忽略透镜间的衍射效应 �5{�X��*�a �`;��cz�;" 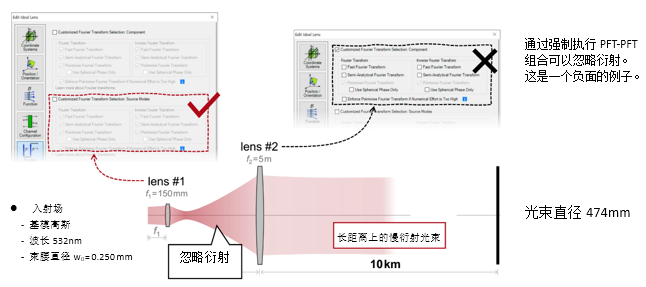 tDt
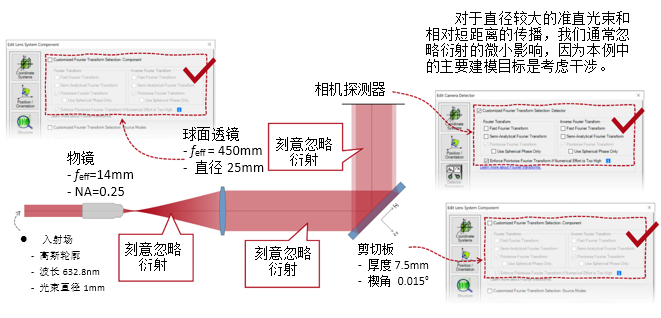
:^�B�c b���]i>Bv� 实例#3:剪切干涉法的准直测试 n]i�yFZ�`9 C��dL��.?^ 1. 例#3:刻意忽略衍射 �@$c!�/��� K{�2h9 ]VF
tDt
:^�B�c b���]i>Bv� 实例#3:剪切干涉法的准直测试 n]i�yFZ�`9 C��dL��.?^ 1. 例#3:刻意忽略衍射 �@$c!�/��� K{�2h9 ]VF 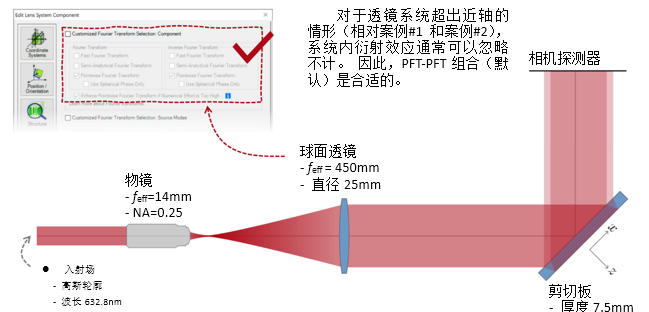 3ev��-Iqz� ��= �^s$
< #w|�5�jN�?
3ev��-Iqz� ��= �^s$
< #w|�5�jN�?
=k_Uj�wgN^
 )~dOmfw%|�
)~dOmfw%|� 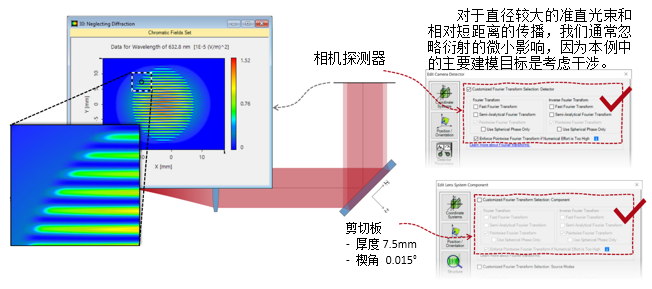 |IN[��u�Q 2. 实例#3:包含衍射 j��^�n�u�| ~�b6GrY"vB
|IN[��u�Q 2. 实例#3:包含衍射 j��^�n�u�| ~�b6GrY"vB 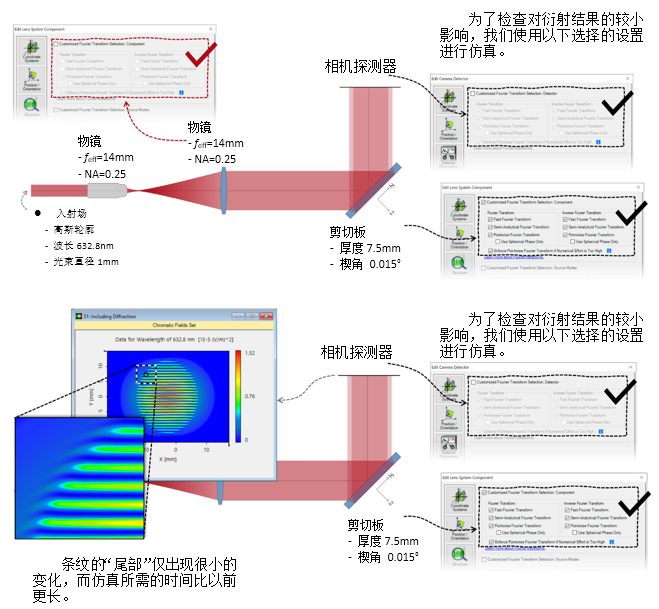 �V^sc1ak1Q
�V^sc1ak1Q