VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接,实现复杂
系统的建模,x域和k域之间的转换是至关重要的一步。 在本文中,我们将通过不同
实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。
=H�Mmrmz: i��|%���5�  \k�;U}Te<� 6�)ycmu;!$ 2. 三种傅里叶变换 U�h.Sc:trA ;�+
��G�9- Te;�gVG�*�
\k�;U}Te<� 6�)ycmu;!$ 2. 三种傅里叶变换 U�h.Sc:trA ;�+
��G�9- Te;�gVG�*� 快速傅里叶变换(FFT)
z5 Bi=~=#� - 对于不同数值计算,一种
标准而高效的算法。
��}w@gj"\H 半解析傅里叶变换(SFT)
h4��Ia>^@� - 一种无需近似的高效重构。
=O,JAR�"ug - 二次相的解析处理,类似chirp-z变换。
�~n6[$WjZA Y;,Hzmbs6w 逐点傅里叶变换(PSF)
�~Eq��\�DK - 受静态相位理论启发的一种近似方法,但采用纯粹的数学形式来表达。
('�t kZt%8 - 对强波前相位是一种高效而精准的方法。
"�x&3Z@q7 JvkL37^�n: �.�|uLt J  Y�dI�0E � ��&3Tx@XhO 3. 每个元件的设置 8%[HYgd5)� _UkmY��Z�/ g�LIT�;B�K
Y�dI�0E � ��&3Tx@XhO 3. 每个元件的设置 8%[HYgd5)� _UkmY��Z�/ g�LIT�;B�K 傅立叶变换设置
Jf)3<� ~�G - 对于每个元件和
探测器,都可以使用 “傅立叶变换”选项卡。
cOkgoL�" 4 - VirtualLab Fusion自动选择所有激活的傅立叶变换选项;不选择未激活的选项。
, H2Yp�Zk - 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况)
~GG���?�GB <�qhBc:kc� 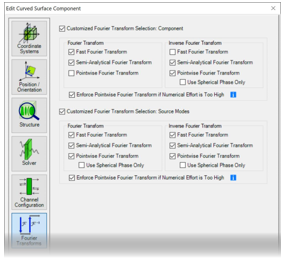 [T`}�yb@�� �S5_t1wqBJ 4. 每个元件的设置 u� g�\�w\b �5��lTD]d�
[T`}�yb@�� �S5_t1wqBJ 4. 每个元件的设置 u� g�\�w\b �5��lTD]d� 傅里叶变换设置
#dc1pfL!y{ g�D�C�OLDM 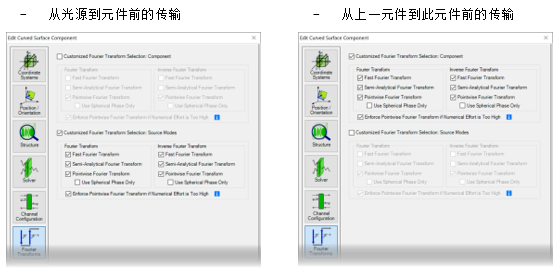 M^6$
M��Mx � � \&a.}t 5. 默认的傅里叶变换设置 :[��sOKV i iq6a��|XGi �WA.�AF�t
M^6$
M��Mx � � \&a.}t 5. 默认的傅里叶变换设置 :[��sOKV i iq6a��|XGi �WA.�AF�t
光源模式和探测器的设置
kn���T.�l" - 对于光源模式和探测器,默认情况下将激活所有三个傅里叶变换选项。
EvE,D��m?h - 在特殊情况下,对于光源模式或探测器而言,
衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。
[;K��mT{I9 �kq�-6�HDR 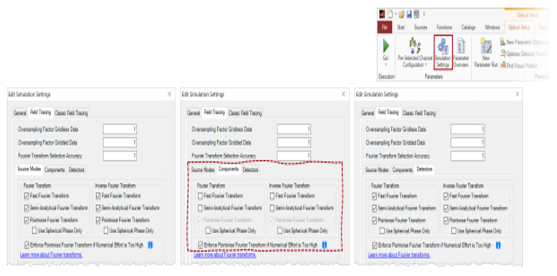 k=/e�M$": E�fiU$�8y� 6. 特殊情况 S�d�d9Dv?! ��XoR>H4xh �7byCc_,��
k=/e�M$": E�fiU$�8y� 6. 特殊情况 S�d�d9Dv?! ��XoR>H4xh �7byCc_,�� 多表面元件
K>1X}ZMdD( - 对下列情况应当特别考虑
xd�8
*<,Wj •透镜系统元件
�Bux�'�hc� •球面
透镜元件
8$vK5�Dnn8 - 此类组件可以理解为
o>c�^�aRZ{ •一组曲面元件,以及
d���T�GA5c •之间有一些自由空间
KWhZ� +i`� - 傅立叶变换选项也会影响介于两者之间的自由空间传播。
T&xt`�|��� }Qr�ab�#v� 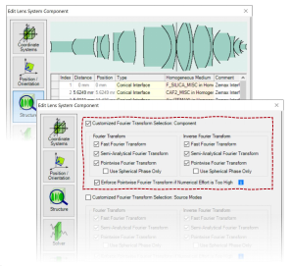 �k\N4@U�K� �(][LQ6�Pc
�k\N4@U�K� �(][LQ6�Pc 在k域的元件
:Q@�)*k�QH - 当元件的求解器/函数在k域中工作时,傅立叶逆变换选项不会产生任何影响
0oU=Rb�C�� - 这适用于以下情况
�;/LD�)$�_ •平面表面元件
X=��~V6m� •分层介质元件
�`�cr(wdvI •光栅元件
.�_�C�P%
R •功能
光栅元件
Dj�Hp+�TyT mm[SBiFO�\ 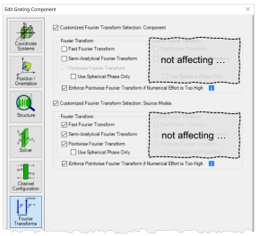 j�m3G?Vn�q GXX+}=b7qO 实例#1:低菲涅尔数系统中的针孔 V U~Dk);Bv /#S>sOg2xq
j�m3G?Vn�q GXX+}=b7qO 实例#1:低菲涅尔数系统中的针孔 V U~Dk);Bv /#S>sOg2xq 1. 实例#1:
成像的光源模式
xx8U$�,N�g E��\{<��;S  ~�xyw>m+o. Owf.f;�Q�R #S5`P�d!�I 2. 实例#1:系统内部包含的衍射效应 n56;m`�IU� ��>dQ�K.CG
~�xyw>m+o. Owf.f;�Q�R #S5`P�d!�I 2. 实例#1:系统内部包含的衍射效应 n56;m`�IU� ��>dQ�K.CG 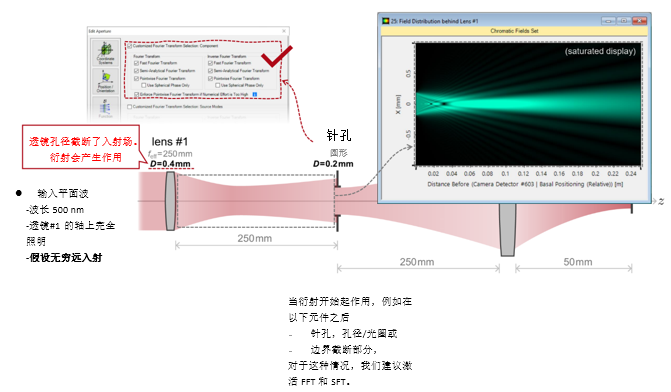 ��8`v$l�iH
��8`v$l�iH 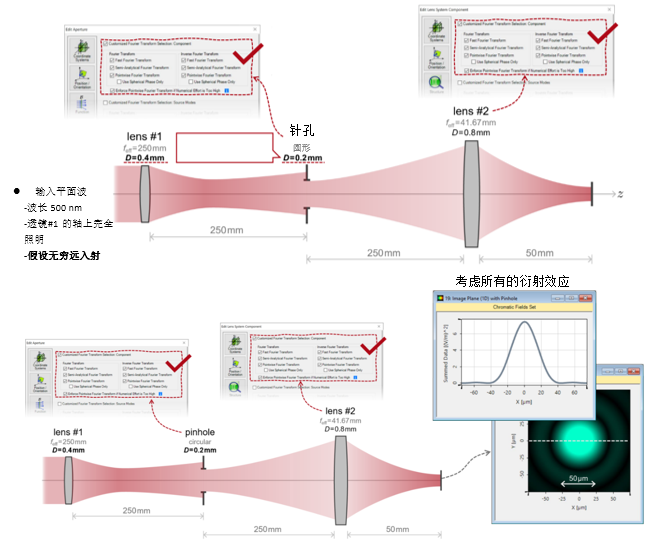 PR�s@��zkO �x��<B'.3y 3. 实例#1:出瞳衍射法 uDuF�#3
+" .g% Y@r)=5
PR�s@��zkO �x��<B'.3y 3. 实例#1:出瞳衍射法 uDuF�#3
+" .g% Y@r)=5 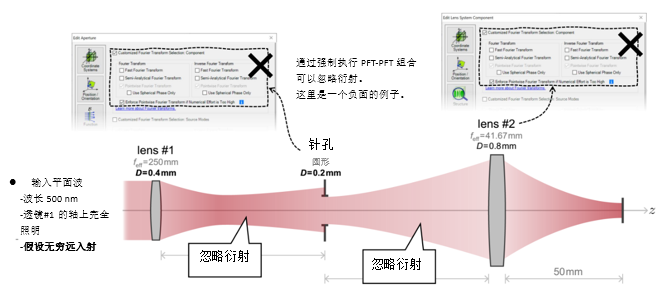 A^�Cj�1:,�
A^�Cj�1:,� 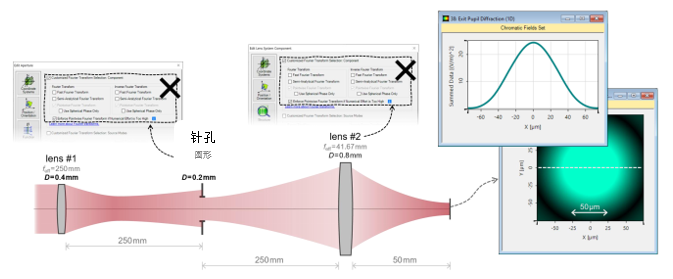 j�o98
jA<� 4. 实例#1:出瞳衍射与对比 >V;�,#5�F_ 3HiFI�SA�*
j�o98
jA<� 4. 实例#1:出瞳衍射与对比 >V;�,#5�F_ 3HiFI�SA�* 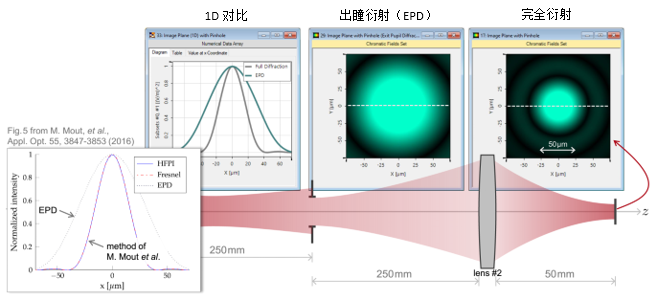 Q M���1F?F $�.K?N@(�W 实例#2:用于激光导星的无焦系统 Lz4eh�WntO M{�N(�~q�l 1. 实例#2:包含所有可能的衍射 K7�`YJp�`i
Q M���1F?F $�.K?N@(�W 实例#2:用于激光导星的无焦系统 Lz4eh�WntO M{�N(�~q�l 1. 实例#2:包含所有可能的衍射 K7�`YJp�`i
�. (`3JQ2s
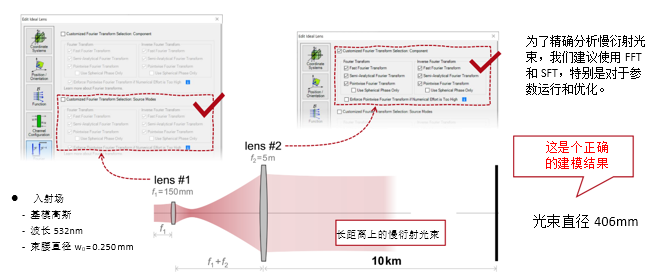 �HJhH-\{@� :w-`PY�J%G y' x���F0� 2. 实例#2:忽略透镜间的衍射效应 :q+N&�j'3� >n��n�Y:7m
�HJhH-\{@� :w-`PY�J%G y' x���F0� 2. 实例#2:忽略透镜间的衍射效应 :q+N&�j'3� >n��n�Y:7m 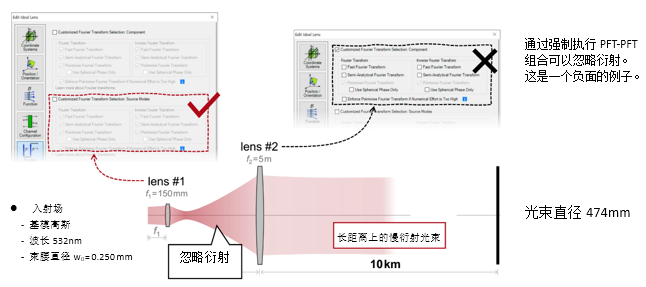 3�071���:W X
K>�&$<5{ 实例#3:剪切干涉法的准直测试 �$v27]"]�� 3/go��Cg�� 1. 例#3:刻意忽略衍射 k�#)�Ad*t� �G<qIY&D�'
3�071���:W X
K>�&$<5{ 实例#3:剪切干涉法的准直测试 �$v27]"]�� 3/go��Cg�� 1. 例#3:刻意忽略衍射 k�#)�Ad*t� �G<qIY&D�' 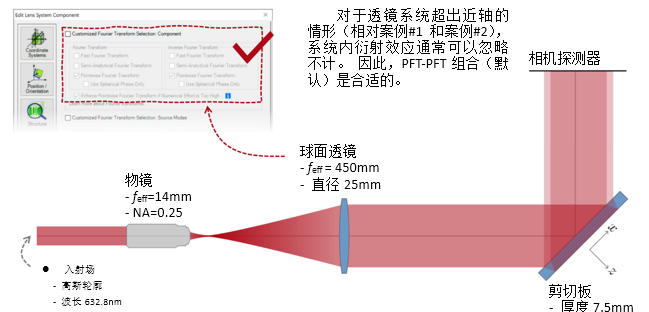 rPiNv
30L� �q<{NO/M�m O\beKBT��;
rPiNv
30L� �q<{NO/M�m O\beKBT��;
����F 3RB�
 �jqcz\n d�
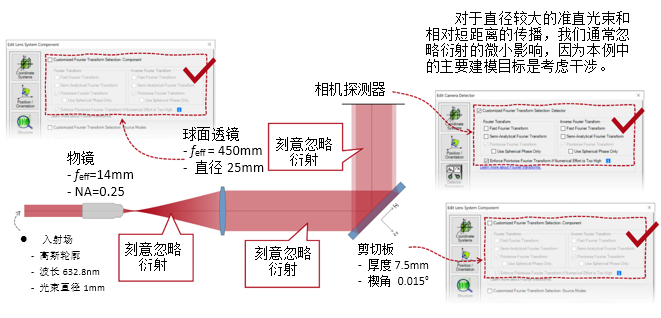
�jqcz\n d� 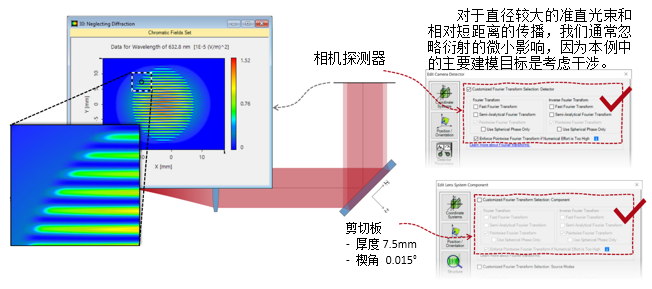 P-S���u5F 2. 实例#3:包含衍射 �E{Vo�'!LY �SUdm� 0y�
P-S���u5F 2. 实例#3:包含衍射 �E{Vo�'!LY �SUdm� 0y� 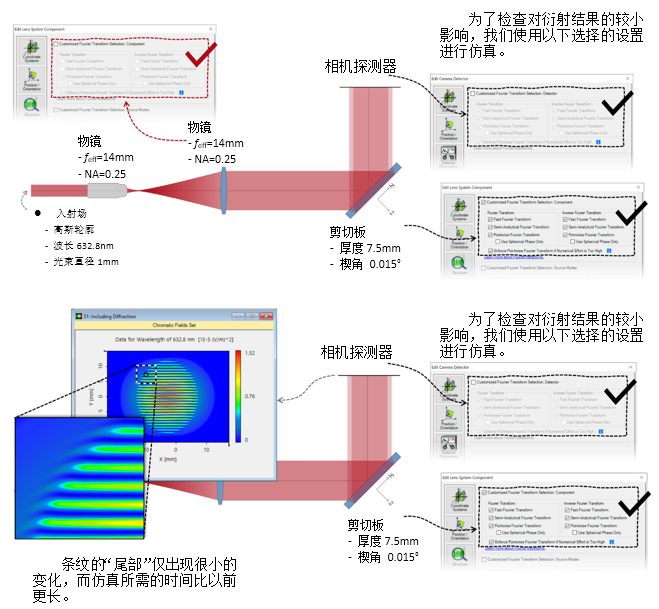 �RKkGI�TDk
�RKkGI�TDk