[技术]傅里叶变换设置——实例讨论 [复制链接]

VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接，实现复杂系统的建模，x域和k域之间的转换是至关重要的一步。 在本文中，我们将通过不同实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。 ,[+gE\z{{u  
kv
SSz%R~  
   SL:o.g(>4  
     t ba%L  
2. 三种傅里叶变换 sBF}j.b  
V#w$|B\  
Y cOtPS%  
 快速傅里叶变换(FFT) +t/VF(!  
        - 对于不同数值计算，一种标准而高效的算法。 if:2sS9r  
 半解析傅里叶变换(SFT) ,_YCl09p(  
        - 一种无需近似的高效重构。 RhbYDsG  
- 二次相的解析处理，类似chirp-z变换。 |...T 4:^Y  
Dw;L=4F |  
 逐点傅里叶变换(PSF) )e9(&y*o  
        - 受静态相位理论启发的一种近似方法，但采用纯粹的数学形式来表达。 |,t#Au}61  
- 对强波前相位是一种高效而精准的方法。 ]Rnr>_>x;  
<+sv
7"a  
         Tp[ub(/;7  
rq}ew0&/  
   t 7;V`[  
3. 每个元件的设置 2}I1z_dq~  
$>5|TG 0i  
49_b)K.tB  
 傅立叶变换设置 O>|Q Zd  
- 对于每个元件和探测器，都可以使用 “傅立叶变换”选项卡。 im%'S6_X4  
- VirtualLab Fusion自动选择所有激活的傅立叶变换选项；不选择未激活的选项。 )"A+T&  
- 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况) +Medu?K `  
G+^HZ4jg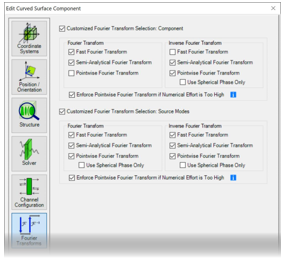  
3HFsR)  
   #=7~.Y  
4. 每个元件的设置 }I,]"0b  
2HkP$;lED  
 傅里叶变换设置 e][U ;  
mm\J]Cc`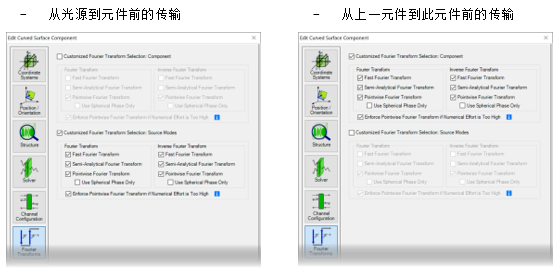  
       5cgDHs  
  (tx6U.O
y  
5. 默认的傅里叶变换设置 N!/^s":  
rMfp%DMA  
CdatN$/*  
 光源模式和探测器的设置 Skp&W*Ai  
- 对于光源模式和探测器，默认情况下将激活所有三个傅里叶变换选项。 ui YZk3  
- 在特殊情况下，对于光源模式或探测器而言，衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。 z~L
(kf4  
>F!2i
b8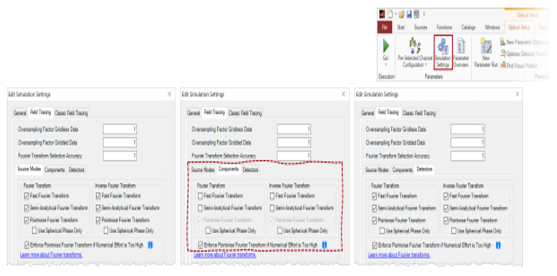  
O|?>rK  
  vkASp&a  
6. 特殊情况 =+'4u  
     MY4cMMjp~  
/*`u(d2g  
 多表面元件 <8+.v6DCd  
- 对下列情况应当特别考虑 FJp~8 x=  
•透镜系统元件 l`~*"4|/  
•球面透镜元件 vv"_u=H  
- 此类组件可以理解为 rrwBsa3  
•一组曲面元件，以及 HKb8z@;%@  
•之间有一些自由空间 k^S=i_ U  
- 傅立叶变换选项也会影响介于两者之间的自由空间传播。 2^E.sf$f  
LylB3BM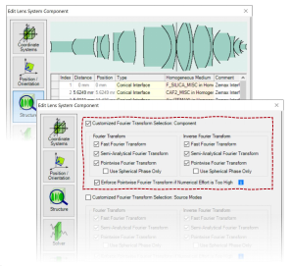  
#fRhG^QKp  
xWU0Ev)4U  
 在k域的元件 /F4rbL^:  
- 当元件的求解器/函数在k域中工作时，傅立叶逆变换选项不会产生任何影响 Q
(T)s  
- 这适用于以下情况 Vqb4 MWW  
•平面表面元件 TmoODG
>@  
•分层介质元件 *y='0)[BD  
•光栅元件 #K"jtAm  
•功能光栅元件 w(eAmN:zR  
ZXFM_>y5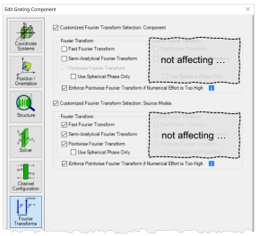  
uv/I`[@HK8  
  4=%Uv^M  
实例#1：低菲涅尔数系统中的针孔 S}cpYjnH8  
C~yfuPr\B  
1. 实例#1：成像的光源模式
XWf8ZZj  
:0Rd )*k,v  
O1ofN#u  
J;Xh{3[vO  
p'0jdb :S  
2. 实例#1：系统内部包含的衍射效应 =%%\b_\L  
^}8(o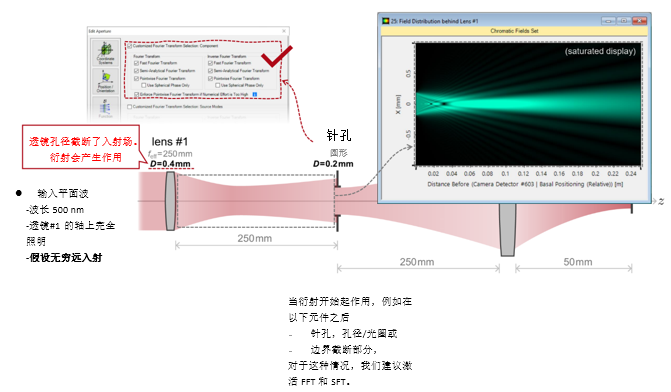  
I_6?Q^_uZ  
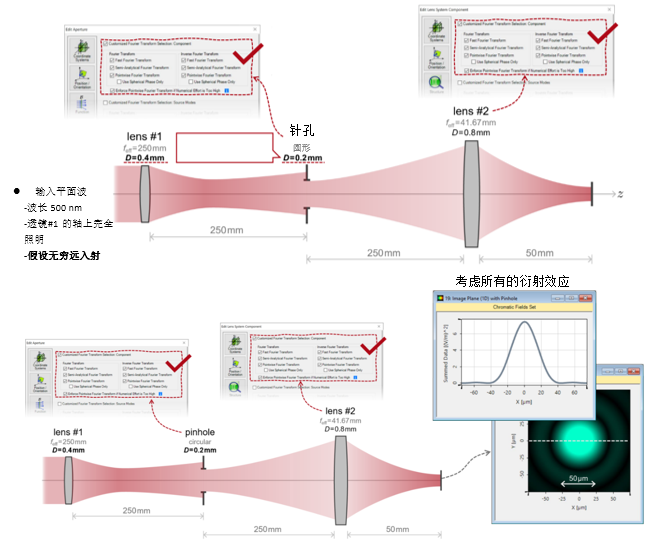zy"L%i  
     'u@
)F`  
3. 实例#1：出瞳衍射法 D}>pl8ke~g  
1j`-lD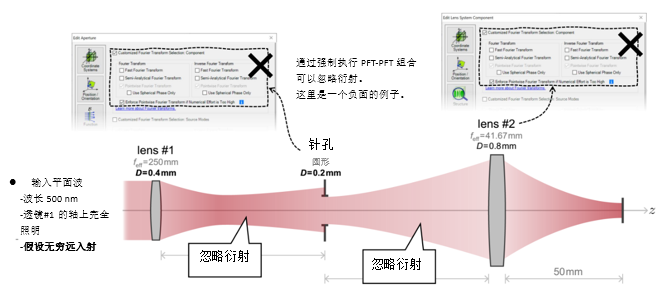  
ug.mY=n'  
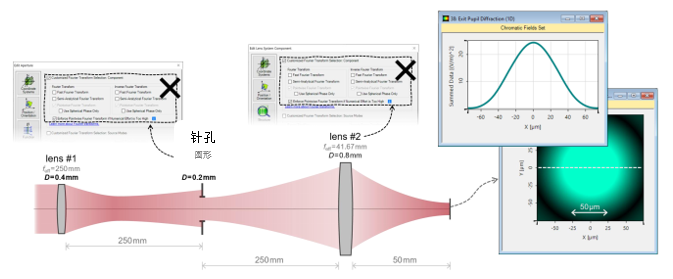rh5R kiF~  
4. 实例#1：出瞳衍射与对比 E5~HH($b  
JN .\{ Y  
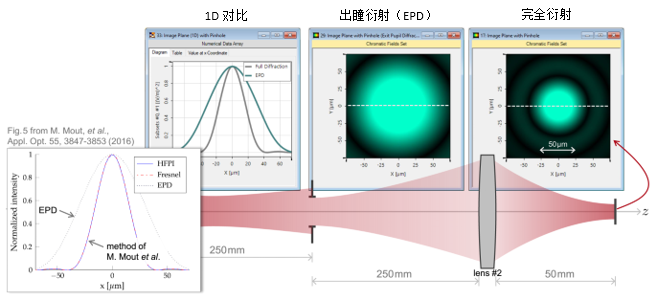'nz;|6uC  
  0~iC#lHO  
实例#2：用于激光导星的无焦系统 }/n
bv;)  
&na#ES$X,  
1. 实例#2：包含所有可能的衍射 %g5TU 6WP  
j&6,%s-M`a  
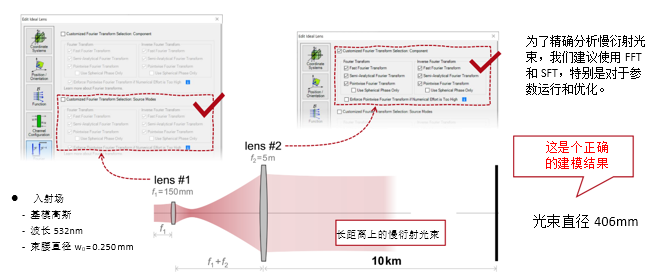D^baXp8  
Kyt.[" p  
puF'w:I(  
2. 实例#2：忽略透镜间的衍射效应 #g#vDR!  
: ^F+mQN  
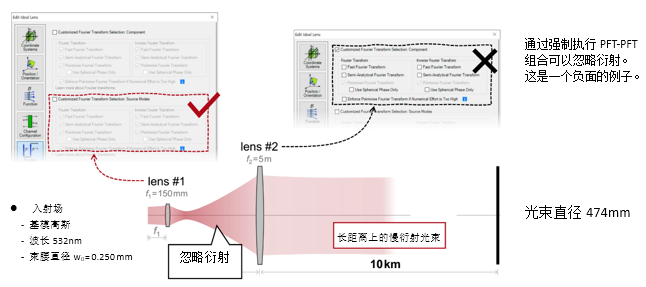GpMKOjVm|  
  5Q#;4  
实例#3：剪切干涉法的准直测试 =Mzg={)v  
@zL)R b%P$  
1. 例#3：刻意忽略衍射 "
w9LQ=mW  
MUhC6s\F  
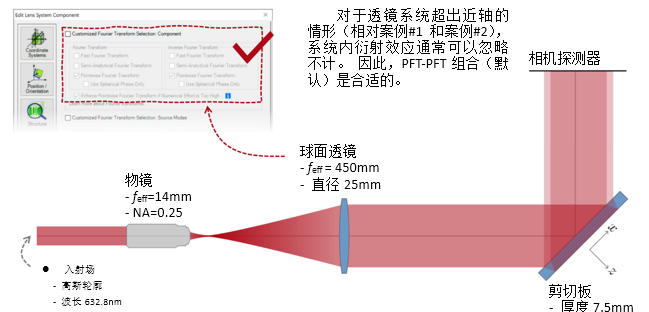\_Nr7sc\  
11glFe  
/ *RDy!m  
&tB|l_p_-p  
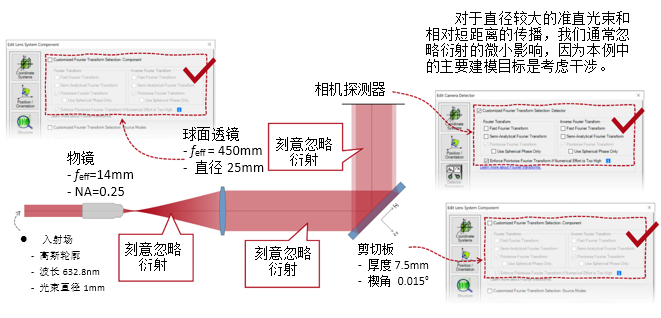A[oLV"J6x5  
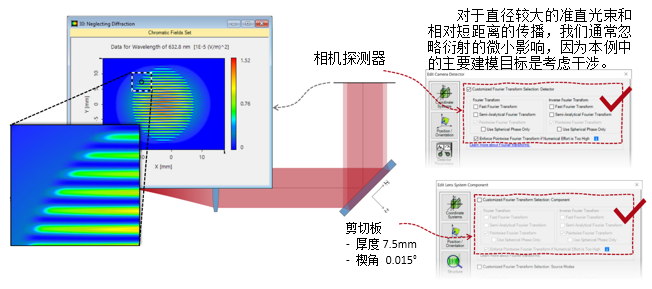4.I6%Bq$  
2. 实例#3：包含衍射 'b:e`2fl  
}__g\?Yf  
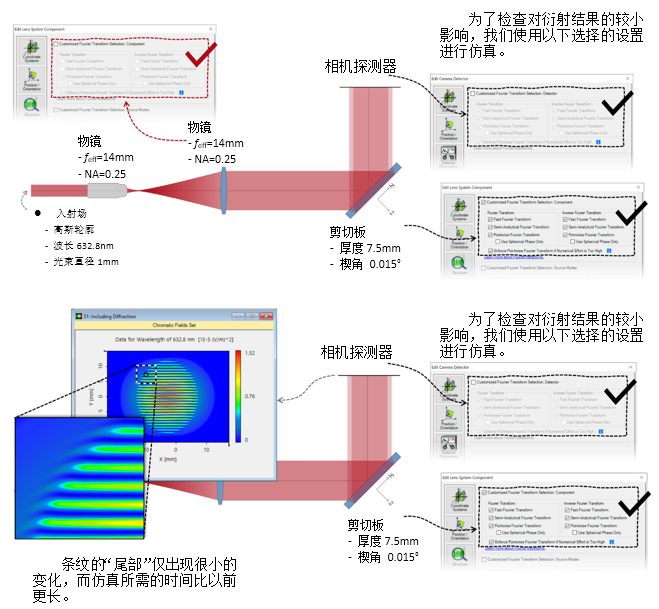7!+kyA\}r^