[技术]傅里叶变换设置——实例讨论 [复制链接]

VirtualLab Fusion包含了多种场求解器和函数。它们可以在空间(x)域或空间频率(k)域工作。为了将不同的求解器和函数简建立连接，实现复杂系统的建模，x域和k域之间的转换是至关重要的一步。 在本文中，我们将通过不同实例的讨论来示范如何对VirtualLab Fusion中有三种傅里叶变换算法进行设置。 z0Z%m@  
W}ofAkF  
   A":T1s  
     Ew$C ;&9  
2. 三种傅里叶变换 ` G kX  
NCD04U5y  
f?)-}\[IR{  
 快速傅里叶变换(FFT) .A|@?p[  
        - 对于不同数值计算，一种标准而高效的算法。 YchH~m
|  
 半解析傅里叶变换(SFT) $Ygue5{c  
        - 一种无需近似的高效重构。 Qv ?"b  
- 二次相的解析处理，类似chirp-z变换。 FC4wwzb  
x|29L7i  
 逐点傅里叶变换(PSF) Gp\ kU:}&  
        - 受静态相位理论启发的一种近似方法，但采用纯粹的数学形式来表达。 -7|H}!DFT  
- 对强波前相位是一种高效而精准的方法。 iJ|uvPCE  
MfkN]\Jyw  
         UL9n-M=  
$NO&YLS@  
   HOJV,9v N  
3. 每个元件的设置 . 'yCw#f  
N)Z?Z+}h  
`QY)!$mUIF  
 傅立叶变换设置 d0 /#nz  
- 对于每个元件和探测器，都可以使用 “傅立叶变换”选项卡。 Ht&YC<X  
- VirtualLab Fusion自动选择所有激活的傅立叶变换选项；不选择未激活的选项。 `qwBn=  
- 傅立叶变换的组合影响自由空间中向前传播过程的建模。(这意味着不仅适用于元件前面的自由空间——它也适用于具有复杂通道配置的情况) 
kvj#c  
9Gz=lc[!7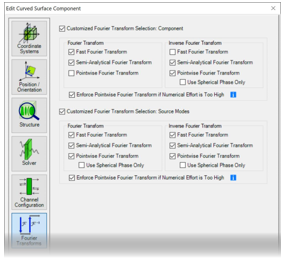  
xd0 L{ue.  
   (4-CF
3D  
4. 每个元件的设置 \.}c9*)  
^dxTm1Z  
 傅里叶变换设置 BD7Ni^qI$  
Vf1^4t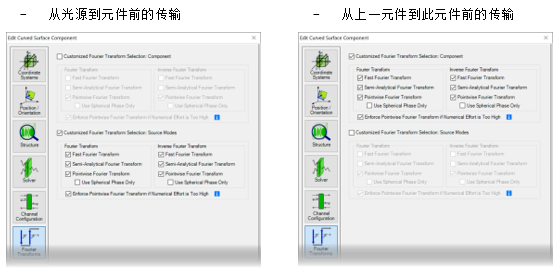  
       EB|}fz  
  [1H^3g '  
5. 默认的傅里叶变换设置 |vzl. ^"-  
{(?4!rh  
|e0`nn
=  
 光源模式和探测器的设置 7cMv/g^h@  
- 对于光源模式和探测器，默认情况下将激活所有三个傅里叶变换选项。 3T0"" !Q  
- 在特殊情况下，对于光源模式或探测器而言，衍射可能无关紧要。 我们将在下面的示例#1和示例#3中讨论这种情况。 28u_!f[  
UR5`ue ;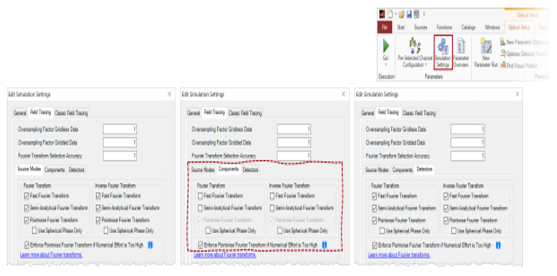  
{+b7sA3
 
  r:TH]hs12+  
6. 特殊情况
<QGXy=  
    
h!9ei6  
S
`Rs82>  
 多表面元件 kg\>
k2h  
- 对下列情况应当特别考虑 |(^PS8wG  
•透镜系统元件 <ZR9GlIr  
•球面透镜元件 UkGCyGyZ[  
- 此类组件可以理解为 Y\'}a+:@Ph  
•一组曲面元件，以及 Fv`,3aNB  
•之间有一些自由空间 `~q<N  
- 傅立叶变换选项也会影响介于两者之间的自由空间传播。 vY`s'%WV  
;YL i{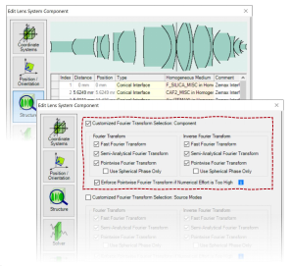  
lqpp)Cq  
/; 85i6  
 在k域的元件 El"Q'(:/U  
- 当元件的求解器/函数在k域中工作时，傅立叶逆变换选项不会产生任何影响 '@P^0+B!(.  
- 这适用于以下情况 +X]vl=0  
•平面表面元件 ENY+^7  
•分层介质元件 -d:Jta!}{  
•光栅元件 l%i+cOD  
•功能光栅元件  %D "I  
o2\8OxcA  
Wo=jskBrQ  
  &b& ,  
实例#1：低菲涅尔数系统中的针孔 QkC(uS  
z*
)T%p  
1. 实例#1：成像的光源模式 0_t!T'jr7  
'1/i"yoW  
7. ;3e@s  
D.XvG_  
BIL Lq8)  
2. 实例#1：系统内部包含的衍射效应 ;sFF+^~L  
J5jvouR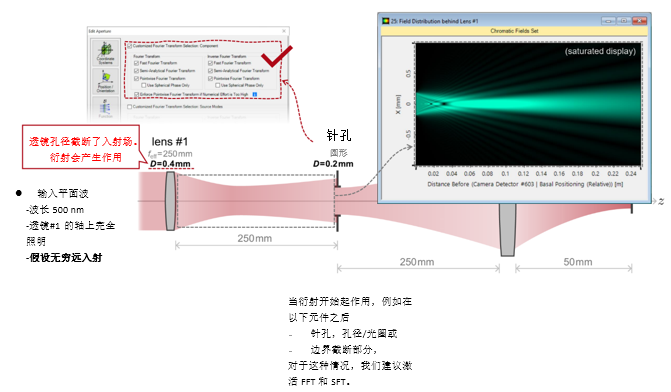  
l1Fc>:o{  
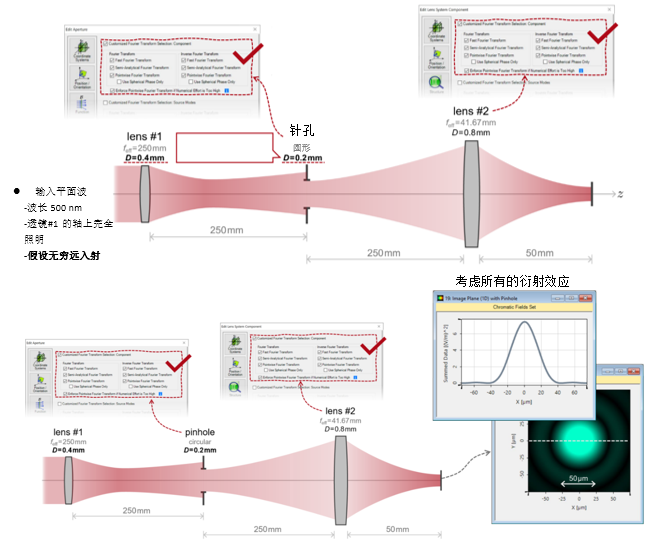.#pU=v#/[  
     k|d+#u[Mj@  
3. 实例#1：出瞳衍射法 hY8reQp1  
SasJic2M  
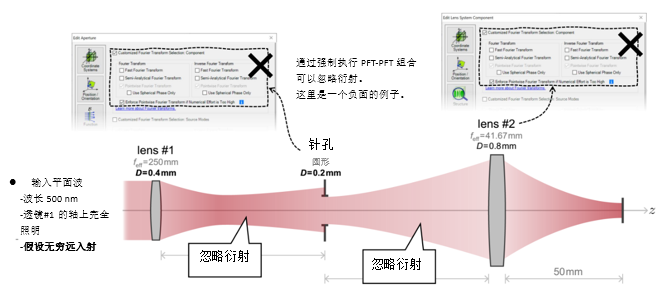*-p}z@8  
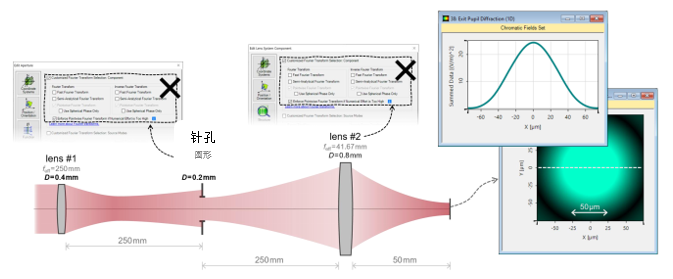.kfIi^z  
4. 实例#1：出瞳衍射与对比 _:27]K:  
h9W^[6  
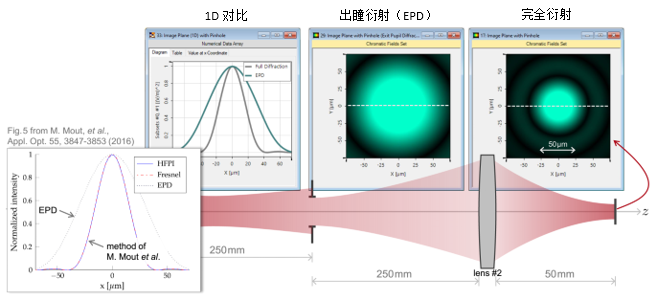!g2+w$YVa  
  6)Lk-D  
实例#2：用于激光导星的无焦系统 "snw4if  
1|wL\I  
1. 实例#2：包含所有可能的衍射 6!FQzFCZq  
~&bq0(  
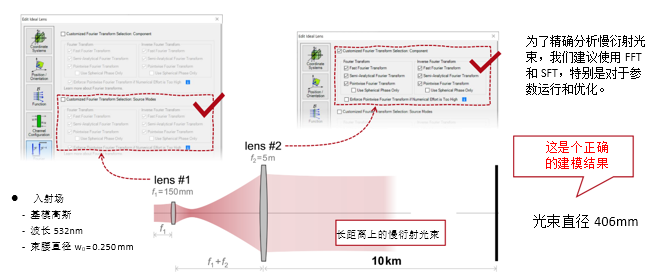HyWCMK6b  
*;*r8[U}q  
y'*K|aTG  
2. 实例#2：忽略透镜间的衍射效应 !C:$?oU  
0lR5<^B  
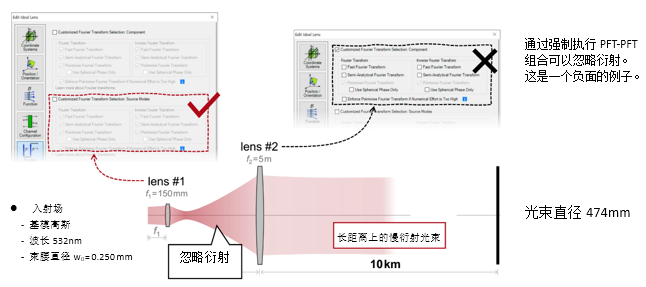~qOa\#x_  
  [cp+i^f  
实例#3：剪切干涉法的准直测试 L;I]OC^J  
CeC6hGR5  
1. 例#3：刻意忽略衍射 }`~+]9<  
sON|w86B  
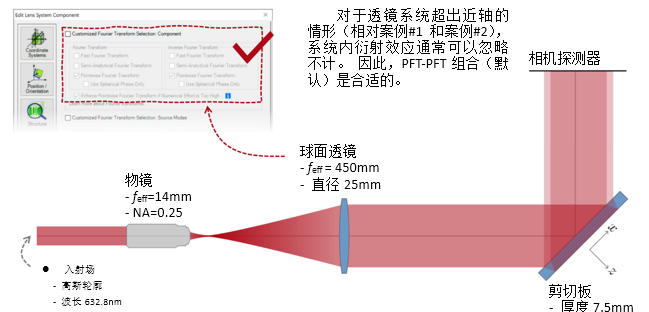d>C$+v>  
%bfQ$a:  
K(Bf2Mfq  
ixD)VcD-f  
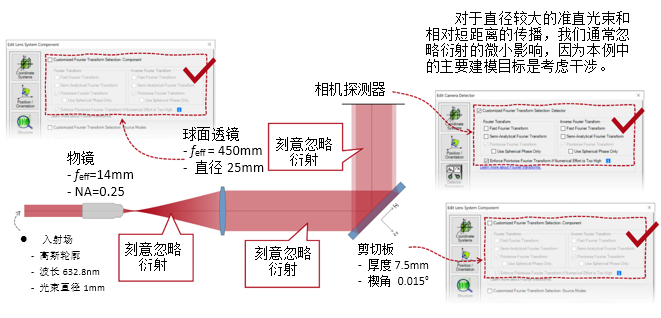w+CA1q<  
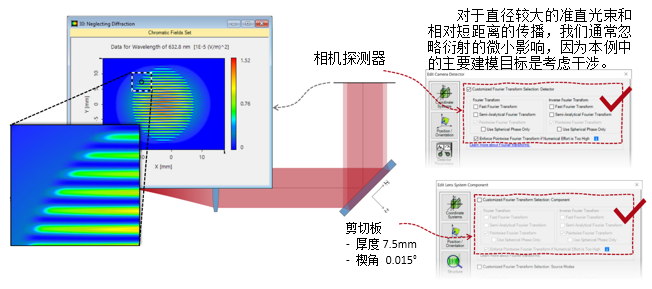kW&TJP+5*  
2. 实例#3：包含衍射 +; AZ+w]ZF  
:20W\P<O!A  
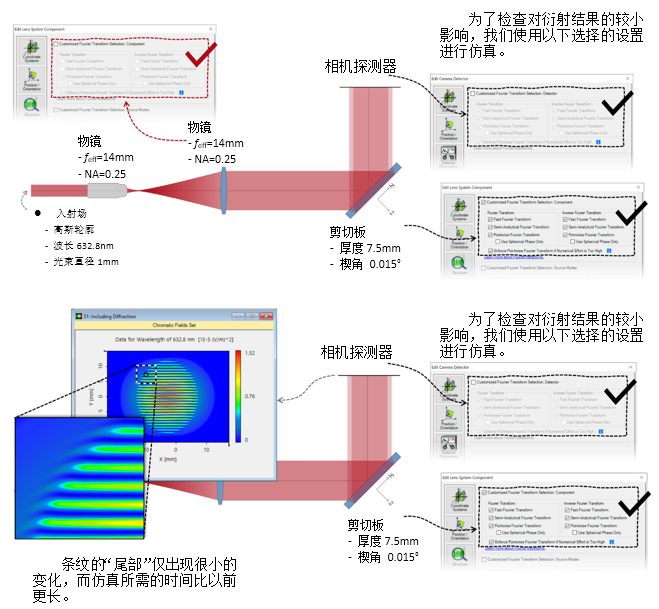Jg|XH L)