切换到宽版
  • 广告投放
  • 稿件投递
  • 繁體中文
    • Zemax光学设计从入门到精通 Zemax光学设计从基础到实践 Zemax光学设计实践基础(陈家璧) ZEMAX光学系统设计实战
    讯技光电:VirtualLab Fusion独家供应商 光学设计与光学元件 CODE V,LightTools,RSoft,LucidShape 计算光学带来的成像革命
    发帖 回复
    返回列表
    • 1002阅读
    • 0回复

    [技术]Savitzky-Golay滤波函数 [复制链接]

    		 上一主题 下一主题
    在线infotek
    科学家
     
    发帖
    6062
    光币
    24463
    光券
    0
    只看楼主 倒序阅读 楼主  发表于: 2022-04-27
    ;9rQN3J$gn  
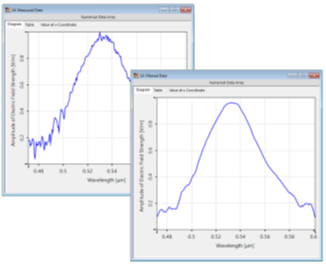
    在测量信号或数据的情况下，很难(如果不是不可能的话)完全避免所有可能的噪声源，因为这些噪声源会干扰任何实验测量。但是，噪声的存在会干扰数据的重要特征(例如，测量光谱的半宽谱)。 wvfCj6}S &  
    因此，有一些后期处理技巧可能会有所帮助。这里我们只讨论一个这样的工具:Savitzky-Golay滤波器，它通过对一组采样点执行回归算法来平滑局部噪声。在这个例子中，我们讨论了VirtualLab Fusion中这个特性的选项和效果，并以一个绿色LED灯在60 nm带宽下发射的光谱为例进行了测试。 6;VlX,,j  
    )]>9\(  
     iS{)Tll}&  
    3.>jagu  
    2.如何进入Savitzky-Golay过滤器 r`5;G4UI  
    s;A]GJ  
    @9^kl$  
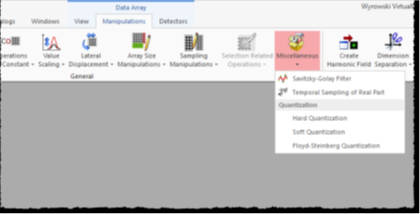
    对于每个实值数据数组，都可以在下面找到Savitzky-Golay滤波器 `ul"D%  
    操作→ ym:JtI69   
    杂项→ r`lgK2r\  
    Savitzky-Golay过滤器 !-: a`Vs+  
    a].Bn#AH!C  
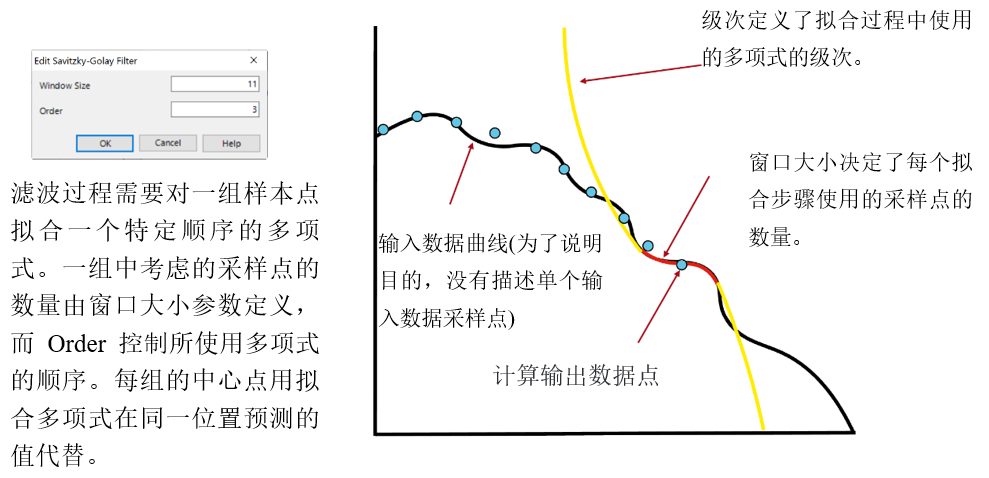
     u*"tZ+|m  
    1~j.jv$  
    3.可视化的过滤函数 &Zov9o:gx  
    v5&WW?IBQ  
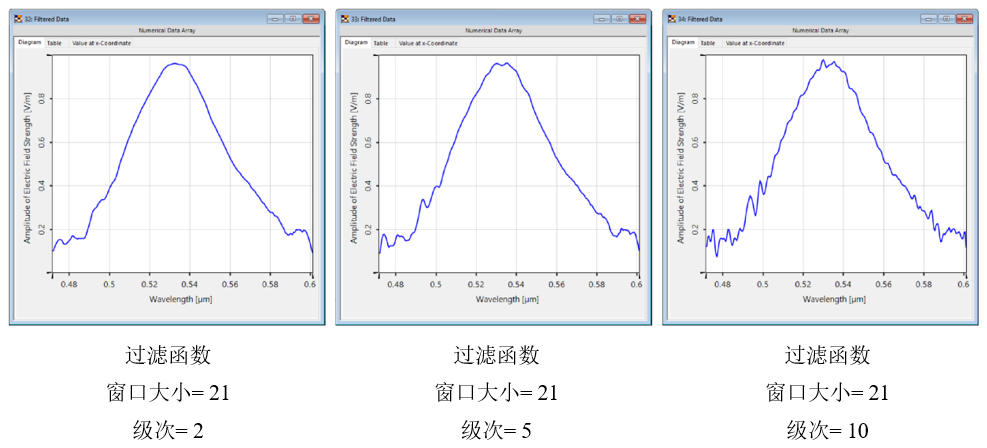
     ! $n^Ze2 !  
    am`eist:  
    4.影响过滤器-窗口大小 L%fWa2P'  
     U5Rzfm4  
    更大的窗口大小导致在拟合过程中考虑更多的采样点，因此曲线更平滑。 9~N7hLT  
    fY>\VY$>  
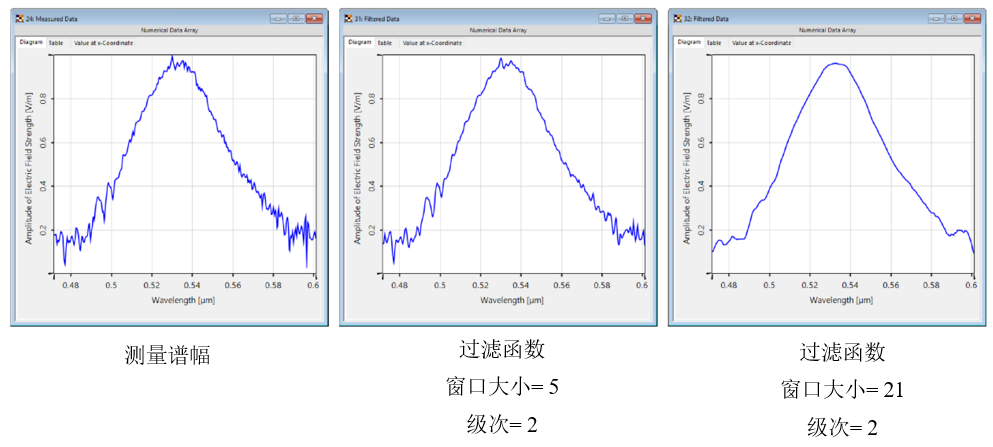     &98qAO]Z  
    ]SK(cfA`  
    更高的阶数允许更详细的曲线，但反过来也可以保留局部噪声。 DRw%~  
    ow+NT  
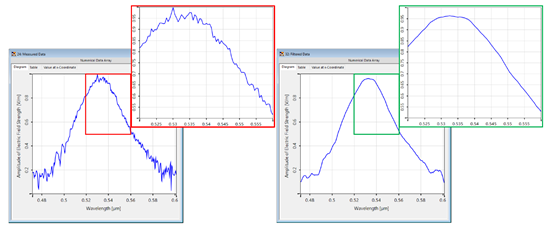
     h1,J<B@  
    Y~Zg^x2  
    5.局部噪声过滤 2t_E\W7w+  
    #* w$JH  
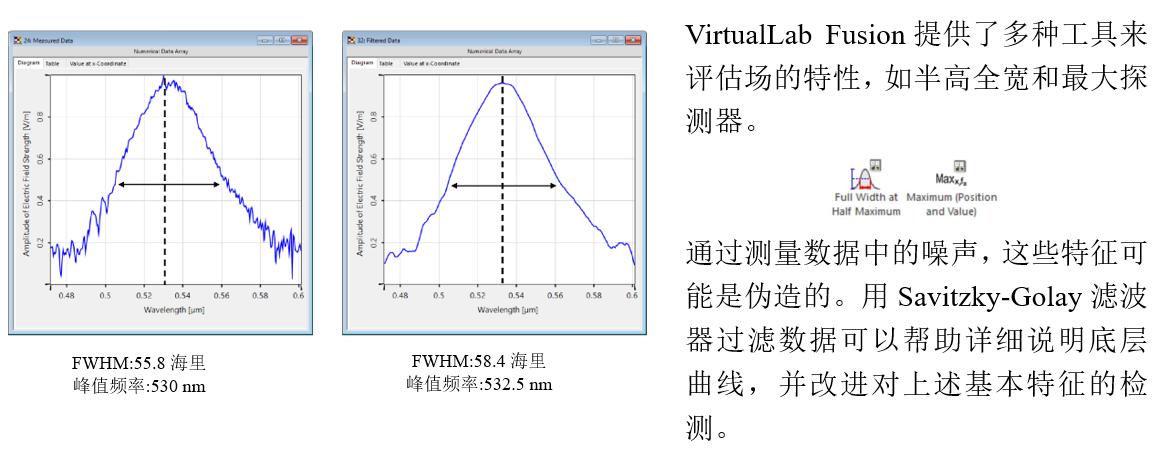
     \2 W( >_z  
    2-2'c?%  
    6.FWHM 检测 Z$2mVRS`c  
    SJw0y[IL6(  
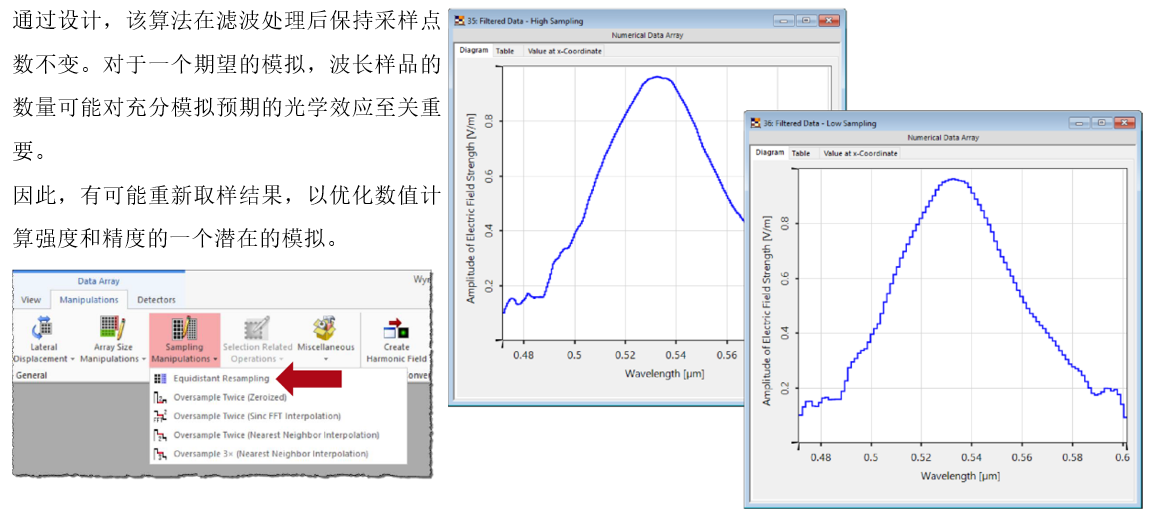
     MECR0S9  
    Yzd-1Jvk  
    7.等距的重采样 Oi7|R7NE  
    XxV]U{i!  
     #E>f.:)  
     
    回复
    举报
    分享到
    发帖 回复
    返回列表