-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-03
- 在线时间1925小时
-
-
访问TA的空间加好友用道具

|
以下我们使用一个很简单的共振器范例模型进行功能示范 ���'$�%�l7 此范例将会示范如何使用GLAD。我们将使用resonator.inp这个档案示范共振器。即使使用者对共振器不感兴趣,这个范例也将会展示在GALD中解决问题的几个重要步骤: j+��
�0I-p
初始化计算机数组及单位 o�:Sa,
!DK
选择波长 Jr�RH\+4K
定义初始分布 :!�!at�:�>
使用宏进行重复运算 8��c^�T�T&
建立数据显示计算结果 Y�glmX"fLf
此共振器将使用半对称的结构进行计算,由半径50cm的球面镜及平面镜所组成。共振器的长度为46cm。输出将由平面镜输出。下表1显示其结构参数: + @s�"zp;F 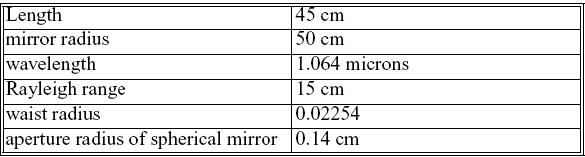 RdR�p�.pb8 RdR�p�.pb8 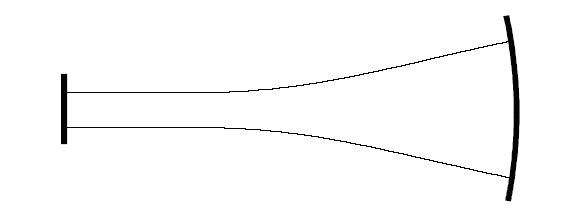 �*wB�1�,U{ 图1-稳定的共振器结构。其光腰将会在平面镜上形成,及其相曲率将与曲面镜的理想模态曲率相同 %/�#N�K1&M 为了简化讨论,我们将忽略增益及形成bare-cavity分析。我们开始分析从准备一个命令档案如下: _^�%�,���x variab/dec/int pass ExL0?FemWV �*wB�1�,U{ 图1-稳定的共振器结构。其光腰将会在平面镜上形成,及其相曲率将与曲面镜的理想模态曲率相同 %/�#N�K1&M 为了简化讨论,我们将忽略增益及形成bare-cavity分析。我们开始分析从准备一个命令档案如下: _^�%�,���x variab/dec/int pass ExL0?FemWV
macro/def reson/o ��N� U���`
pass = pass + 1 # increment pass counter VQ9/Gxd�eo
prop 45 # propagate 45 cm. l�p%pbx43s
mirror/sph 1 -50 # mirror of 50 cm. radius �C1 GKLl�~
clap/c/n 1 .14 # .14 cm. radius aperture ^yN&�ZI3P&
prop 45 # propagate 45 cm. along beam t=W��}S��H
mirror/flat 1 # flat mirror 57']#j#"hj
variab/set Energy 1 energy # set variable to energy value [j/9neay�e
Energy = Energy - 1 # calculate energy difference h�y"�\�RW�
udata/set pass pass Energy # store energy differences UJ')I`zuI�
energy/norm 1 1 # renormalize energy fSvM(3Y<Qh
plot/l 1 xrad=.15 # make a plot at each pass �:(*�V?WI
macro/end �9 X`�Sm}i
array/set 1 64 # set array size �jLHkOk5{:
wavelength/set 0 1.064 # set wavelengths @>Km_A���x
units/set 1 .005 # set .005 cm sample spacing �"n5N[1b�k
resonator/name reson # set name of resonator macro d�n$!&����
resonator/eigen/test 1 # find resonator properties Gm^U;u}=�f
resonator/eigen/set 1 # set surrogate beam to eigen mode |~mOfuQ�b
clear 1 0 # clear the array E�Dl�!�w�:
noise 1 1 # start from noise j/c�&xv�7=
energy/norm 1 1 # normalize energy s�L�T3Y}IO
pass = 0 # initialize pass counter u�o�%)1NS!
reson/run 100 # run resonator 100 times !P��fr�,�a
title Energy loss per pass q Y?�j#fzi
plot/watch plot1.plt # set plot name Pw`8���Wj�
plot/udata min=-.05 max=.0 # plot summary of eigenvalues �w�;:*���P
title diffraction mode shape IDriGZZ<)6
set/density 32 # set plot grid to 32 x 32 E�,x+Je�KV
set/window/abs -.05 .05 -.05 .05 # set plot window ��YWO)HsjP
plot/watch plot2.plt # set plot name �9W1YW�9rL
plot/iso 1 # make an isometric plot �ag;pN*��z
以下就对每一项指令来做介绍: jZkc�BIK2�
variab/dec/int pass H;k~oIs�k�
此行定义一整数变量叫pass。我们将使用pass来储存数据,变量如果不清楚的定义为整数,将会被定义为实数变量。 9Uekvs=r=M macro/def reson/o >7T��'��OC
此行开始定义宏,就像是子程序或函式一样。所有介于macro/def与macro/end之间的指令都将定义为宏。这些指令暂时不会被执行。这些指令列将被放在MACLIB中留待以后使用。这些宏指令列将不需缩排。但使用缩排将会使这些指令更容易阅读。 k|�PN0�&�J pass = pass + 1 # increment pass counter ]�dmr�kZz:
此行将pass变数加一。这是一个简单的数学式。我们使用pass来计算执行宏的次数。#字符表示其后的字为批注。当我们在下指令时使用批注是很重要的一件事。 E�e��%�%�d prop 45 # propagate 45 cm. 5 ,B_u%b�b
此行表示绕射传播45cm。绕射传播的计算花费最多的时间。但是,对现代的计算机而言64X64的矩阵运算只是很短的时间而已。 By�",rD- r 此45cm的传播距离是将光线由左边的平面镜,传播至右边的曲面镜如图一。 W�U�Xx;9�> mirror/sph 1 -50 # mirror of 50 cm. radius :g�=qz~2Xk
此行为设定球面镜为曲率50cm。”1”表示设为镜面对光束 1作用。光束最多可达40道,但只有一道用在此一分析中。在指令中的负号表示为一凹面镜。此凹面镜使光线收敛并将光线反向。 .|>3k'<�l� clap/c/n 1 .14 # .14 cm. radius aperture cO+qs[
BQ
此一指令建立一圆形的0.14的孔径对光束1作用。孔径是非常重要的在共振器中,它大量的减少了散射光线。并且,孔径将光束减为剩下最少的模态。 Y0�dEH�^�I prop 45 # propagate 45 cm. along beam '� ;F�nI�Z
此为第二次传播将光束由右边的球面镜向左传播回平面镜。 DG�n;m\B� mirror/flat 1 # flat mirror E�i�b5���
建立一平面镜在左边针对光束1。对bare-cavity共振器分析,光束只是直接反射回右边。在真实的雷射中,镜面将会是部份反射让光束传播出去。 a�;qr�yUyG variab/set Energy 1 energy +R�M�SA��^
变数Energy设为光束1的总能量(真实能量)。我们没有将其定义为实数变量,但在GLAD中将会自动设为实数变量。 -[�9JJ/7y
Energy = Energy - 1 # calculate energy difference Q�}K"24`=
此算式将能量减1计算每次传递所损失的能量。 G3vxjD<DMW udata/set pass pass Energy # store energy differences �P90��y��I
此处使用udata这个指令将Energy数据存入数组中,使用两个pass变量,分别为数组的横坐标及纵坐标。 '��ud{m[|� energy/norm 1 1 # renormalize energy li'YDtMKCY
此行将共振器中的能量归一化。在真实的雷射中,能量被孔径及其它效应所损失,以及被其它放大器的能量增幅,在稳定态时所平衡。在bare-cavity分析中,就像我们在这里所做的,我们模拟拟稳定态增益简化为将增益值做再归一化,在每次传播的最后。 J~�zU�p(>K plot/l 1 xrad=.14 # make a plot at each pass '/n�1I�M$7
画出空腔分布使用等比例的绘图显示模态形式对时间的关系图。 �6"5A%{�J� macro/end 8h�z^%�v�m
结束宏定义 :v�qgGKml$ array/set 1 64 # set array size Ls$D$/:q�?
此指令是定义Beam 1为64 x 64的矩阵。此数据为计算的主体,任何尺寸的矩阵都可以被定义。对一个小型的稳定空腔共振器而言,一个小的矩阵已经足够准确,因为只有低阶模态是最重要的。 �FF(#]vz�' wavelength/set 0 1.064 # set wavelengths �PI�:4m%[�
设定Beam 1 的波长为1.06μm �O1U=�X:Zl units/set 1 .005 # set array size �
�Rn(ec�
此行定义数组的尺寸为0.005 cm,所以64 x 64的数组大小为0.32 cm �)�@l�%� resonator/name reson # set name of resonator macro ���+yH7v5W
此行定义共振器的宏名称为”reson” �Ms5ap<q# resonator/eigen/test 1 # find resonator properties �~"&|W'he[
此行进行共振器的测试,得到其基本特性。GLAD使用此一信息来决定所使用的数值算法。使用正确的数值算法是非常重要的,可让我们在每次的传递后得到正确的结果。光束的强度及相位在每次传递后都会改变,但其算法必须保持不变才能得到正确的结果。 2A���azy'/ resonator/eigen/set 1 # initialize surrogate beam v6M6>&R�R|
此处确定光束最初的初级损失模态,藉由此一指令resonator/eigen/set来确定。可以确定用来计算高斯光束的演算已设定完成。我们可以变更光线的资料,在下面两行指令完成后。 �t�~EPn�.� clear 1 0 # clear the array �Vv�n�2 Ep
noise 1 1 # start from noise � gmO���!� 第一行设定整个光线矩阵为零。第二行放入随机数噪声在数组中,仿真自发辐射所造成的噪声影响。 �JPc+r��fF
大部份的雷射都从自发辐射开始,所以此一设定更增加了真实性,而不是简单的平面波而已。当然,稳定态的解不会因为我们的初始条件而有所影响。 k"T}�2 ��7 wOEj�)fp�. energy/norm 1 1 # normalize energy +�mmSfuO&\
此行调整光线的强度,不需要改变其外形,所以其总能量将会是归一化的。我们将会量测能量在每次传递后并减1,此一差异将表示出能量的损失。 V��6&!9b� pass = 0 # initialize variable 9Zt`u,���;
将pass这个变数设为0 �RX�p��w! reson/run 100 \K{����0�L
执行reson此一宏100次,有时候我们会需要执行超过100次或少于100次的执行得到稳定 D3Ig>gKo?m
的效能。 6x�e*E[#k\ title Energy loss per pass u~��M�
q�*
定义下式绘图所使用的标题 Ustv{�:7�v plot/watch plot1.plt # set plot name Yq0�| J��
此指令建立绘图文件名称。绘图数据将会储存在此一档案中。Watch程序会自动的显示绘图数据并自动更新数据,当新的绘图数据建立在同一个文件名称中。Watch将会针对不同的文件名称建立不同的绘图窗口。可以让我们同时观察到许多图形。 jk; clwyz/ plot/udata min=-.05 max=.0 x=hiQ>BIO0
此行画出在宏中使用udata/set所收集的数据。最小及最大值的定义更有效的显示出损失。 i&�Tbz�! title diffraction mode shape |+FubYf�?$
此行定义下图的标题 H�ZzD��VCU set/density 32 # set plot grid to 32 x 32 7a�=gH2]�&
set/window/abs -.05 .05 -.05 .05 zl>nSnd�RE
第一行定义网格线密度为32x32。第二行定义绘图宽度为0.05 x 0.05 cm。此指令让绘图区域正好足够绘出主要的光线部份。 ��3nIU�1e� plot/watch plot2.plt # set plot name eue�H�)Xkf
此行定义新的绘图档案。Watch将会定义新的绘图窗口给新的档案。 w�;[NH/A^a plot/iso 1 ��J{p1|+h%
此行定义等比例图显示共振图的模态在100次的传递后。因为我们开始于随机数噪声,经过100步 �'8RsN-�w
之后并未完全收敛,还有一些低阶的Hermite-gaussian模式存在。如果我们执行更多步计算,终究会得到期待的稳定高斯模态。 L3��u&/Tn2 执行此一档案只要输入read/disk resonator.inp就可执行刚才输入的指令 ��"/*\1v�9 UU�YS�Fa�%
�axv>6�k�� QQ:2987619807 n/�;Wxn�nQ
|