[推荐]GLAD：共焦非稳腔模拟仿真 [复制链接]

采用球面反射镜构造了一个共焦非稳腔，该结构与Siegman和Miller描述的结构一致[1]。该谐振腔的准直菲涅尔数和等量菲涅尔数分别为： ,CM$A}7[  
& bw1  
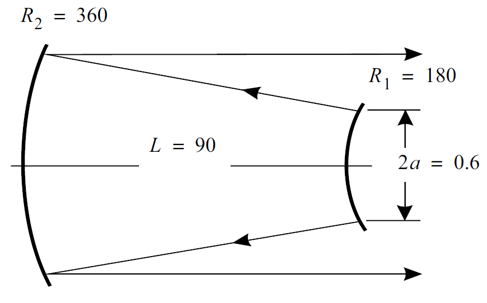
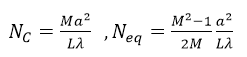     (11.1) [sKdIw_  
其中，a是孔径半径，L为腔长，λ为波长，M是准直倍率。相应的参数数值为:L=90cm，a=0.3cm，M=2，λ=10μ。带入后计算得：N_c=2，N_eq=0.75。 m_Fw;s/9  
4qm5`o\hb  
激光在腔中来回一次后，分布的单位是初始时的两倍。要开始另一次来回传输，单位需要缩放到原来的单位，根据Siegman和Miller理论，每个来回损耗大约为44%。 GF/p|I D  
4a2&kIn  
GLAD的计算与该理论相符甚好。 u5CT7_#)  
D *LZ_  
~C!vfPC  
参考文献 M;43F*  
swLgdk{8
n  
A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). Bxa],inuZ  
Y6D=tb  
%74Ms  
C 谐振腔参数 J0=`n(48B  
---------------------------------------- BgpJ;D+N4  
等效菲涅尔数      0.5 y6PAXvv'{  
放大倍率          2 1 yzxA(  
腔长              90cm C,IN+@  
孔径1半径       0.3cm H`Z4a
N  
孔径2半径      0.6cm s~]nsqLt9p  
----------------------------------------- ^c(PZ,/#JB  
J<`RlDI  
## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 'Yd%Tb|*  
## pass_number变量是为了计数宏运行次数，同时作为标题输入参数 <hK$Cf_  
##变量stop用于测试收敛，并将值传递到if语句以退出宏 ~AE034_N  
###变量field_radius用于在宏结束后初始化数组并重新调整场半径 /e7'5#v  
variable/dec/int pass_number          # 声明pass_number变量为整数 !<YRocQY  
variable/dec/int STOP TEST            # 声明确定收敛的开关 \W(p)M  
PZ ogN  
####定义一个宏，它是一系列命令，通过空腔表示一个循环 mJsYY,b8  
macro/def conres/over     # 声明宏conres /新信息覆盖旧信息 6=@n b3D%  
pass_number = pass_number + 1 list #增量计数器 y1 }d(%  
clap/cir/no 1 .3                        # 孔径1 定义 c~tSt.^WX  
mirror rad=180                       # 凸面反射镜，曲率半径r=180 q;>BltU  
prop 90                              # 向后传播90cm U|Jo[4A  
mirror rad=360.                        # 凹面镜 @Op8^8$`  
clap/cir/no 1 .7                        # 孔径2定义 ,j

t098W  
prop 90 # 向前传播90cm !}3`Pl.(r  
variable/set Energy 1 energy           # 将光束的能量存在变量Energy ./fEx 'E  
write/screen/on  # 写屏 Qrt8O7&('  
udata/set pass_number pass_number Energy-1  #储存光束能量的变化量 E%;'3Qykva  
gain/converge/test ibeams=1 nstore=STOP  # store convergence test in STOP # )Xh_q3=  
gain/eigenvalue/show 1  # 显示本征值 Ov<3?)ok  
energy/norm 1 1  #光束能量进行归一化 7GIv3Dc  
if STOP macro/exit  # 条件退出   gOWyV@  
if [!TEST] then  #TEST值为0， 执行语句 `Eu(r]:W  
title resonator mode pass = @pass_number   4vX]c  
plot/l xrad=.75   ^6LFho4  
endif :O!G{./(_  
macro/end qIqk@u  
a[$.B2U  
###初始化变量 SQ Fey~  
pass_number = 0  # 往返次数初始化为0 # DdQf%W8u  
field_radius = 1.6  #调整场半径 h#n8mtt&i  
L$Leo6<3a  
c##建立初始单位和高斯场分布 6>L.)V  
array/set 1 128  #设置矩阵为128*128 kI
fb!  
units/field 1 field_radius  # 定义单位 QhG-1P3#  
wavelength/set 1 10.  # 定义波长 _5K_YhT  
gain/converge/set eps1=.005 eps2=.001 npoints=3  #能量收敛准则的分数变化设置 8x9kF]=  
nM; G; T  
c#调用宏请求最多30个传递，并在收敛条件下退出 |ber
:1  
gain/eigenvalue/set 1   .3U[@*b(  
plot/screen/pause 3 op|mRJBq;  
TEST = 1   wrO>#`Z  
resonator/name conres  #设置谐振腔名字 R|CY4G j  
resonator/eigen/test 1  #寻找本征值 t@u\ 4bv  
TEST = 0   9V],X=y~  
pass_number = 0  #往返次数初始化为0 8@fDn(]w  
clear 1 0                                  #光束初始化为0 R_qo]WvR;  
noise 1 1                                 #从噪声开始 BH-[q9pf  
resonator/run 30                         #宏运行30次 >#:/ GN?  
title ex 11: energy per step                #设置图形的标题 7XDV=PQ[  
plot/watch ex11a_1.plt    #设置图形窗口的名称 )*A,L%  
plot/udata max=0   #设置横坐标范围 bF KPV%`  
C^%zV>o  
###绘制汇聚场分布 bg,}J/  
title ex 11: resonator pass no. @pass_number  #设置图形的标题 46zaxcY<!  
plot/watch ex11a_2.plt             #设置图形窗口的名称 lz)"zV  
plot/liso 1 xrad=.75 ns=64           ZmULy;{<)  
obs 1 .3                           4v|/+J6G  
title ex 11: outcoupled beam        #设置图形窗口的名称 E~>6*_?  
plot/watch ex11a_3.plt             VRX" @uCD  
plot/liso 1 xrad=.75 ns=64         t>wxK ,  
nP3GI:mjL  
c##应用透镜并传播到远场 7idi&h"  
lens/sph 1 100                   Qsntf.fT  
prop 100                         ?fmt@@]T?  
title ex 11: far-field pattern  #设置图形窗口的名称,画出远场模式 p0rwiBC=q  
plot/watch ex11a_4.plt             O&,O:b:@  
plot/liso 1 ns=64                 3\KII9  
hf<$vRti>  
c###生成环围功率表 Su"_1~/2S  
encircled/calculate/energy 1       A&P1M6Of  
encircled/udata 1                 lk +K+Ra/  
title ex 11: encircled energy       \ZFQ?e,d  
plot/watch ex11a_5.plt # ` (D4gPW  
plot/udata 1 min=0. max=1. # <s-@!8*(  
end |"yf@^kdC  
z/KZ[qH\  
{%_j~  
'Y[A'.*}4  
}Hz-h4Z  
#Q3PzDfj  
e(#IewKp