-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
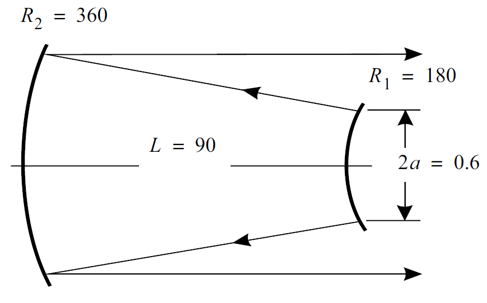
采用球面反射镜构造了一个共焦非稳腔,该结构与Siegman和Miller描述的结构一致[1]。该谐振腔的准直菲涅尔数和等量菲涅尔数分别为: X[SI�k%{�D R+.kwq3CED
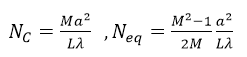 (11.1) 4�C�*�0MV 其中,a是孔径半径,L为腔长,λ为波长,M是准直倍率。相应的参数数值为:L=90cm,a=0.3cm,M=2,λ=10μ。带入后计算得:Nc=2,Neq=0.75。 �u
Qg$h��S (11.1) 4�C�*�0MV 其中,a是孔径半径,L为腔长,λ为波长,M是准直倍率。相应的参数数值为:L=90cm,a=0.3cm,M=2,λ=10μ。带入后计算得:Nc=2,Neq=0.75。 �u
Qg$h��S
�~4m�Rm!DP 激光在腔中来回一次后,分布的单位是初始时的两倍。要开始另一次来回传输,单位需要缩放到原来的单位,根据Siegman和Miller理论,每个来回损耗大约为44%。 ]M�~�7��L[
J�Lg�/fB3% GLAD的计算与该理论相符甚好。 v�0T?c53�?
x<.(fRv �
 Q��"3gvIyc 参考文献 ��6
�tB\X^ C��3
Bo�H& A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). iDl��tN]zS ��}
na@gn� �oqg +�<m� C 谐振腔参数 7=&+0@R#/d ---------------------------------------- 3/]��~#y%2 等效菲涅尔数 0.5 �v`p�@d�jM 放大倍率 2 XQ�tV$�Lw� 腔长 90cm HJ�d{j,�M 孔径1半径 0.3cm �ZQ'�|B� 孔径2半径 0.6cm !�He�QMz�� ----------------------------------------- vTL/%� SJ8 �+k/=L9�#e ## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 Tz�0�XBH_ ## pass_number变量是为了计数宏运行次数,同时作为标题输入参数 z<J2�e^j� ##变量stop用于测试收敛,并将值传递到if语句以退出宏 $)K�Np�dXh ###变量field_radius用于在宏结束后初始化数组并重新调整场半径 a��a�dw#90 variable/dec/int pass_number # 声明pass_number变量为整数 qt4��%=E;[ variable/dec/int STOP TEST # 声明确定收敛的开关 yf�4 i!�~ /Kd'�!lMuz ####定义一个宏,它是一系列命令,通过空腔表示一个循环 (B�v~6tj~J macro/def conres/over # 声明宏conres /新信息覆盖旧信息 0w vA�tK|Q pass_number = pass_number + 1 list #增量计数器 tGS�X�TF}G clap/cir/no 1 .3 # 孔径1 定义 Tl+PRR6D*� mirror rad=180 # 凸面反射镜,曲率半径r=180 ~aXJ5sY"f& prop 90 # 向后传播90cm ��t[A���A= mirror rad=360. # 凹面镜 �q%,y66pFr clap/cir/no 1 .7 # 孔径2定义 �B�A8!NR| prop 90 # 向前传播90cm T�r;&bX5]H variable/set Energy 1 energy # 将光束的能量存在变量Energy h�<n�2pz�} write/screen/on # 写屏 ��y'z9Ya�� udata/set pass_number pass_number Energy-1 #储存光束能量的变化量 �\!%~(�FM gain/converge/test ibeams=1 nstore=STOP # store convergence test in STOP # 8A�u W>7_� gain/eigenvalue/show 1 # 显示本征值 _�lC0XD�Z energy/norm 1 1 #光束能量进行归一化 ^g.H�JQ'vF if STOP macro/exit # 条件退出 ]��L�MtZUz if [!TEST] then #TEST值为0, 执行语句 qc���a=a�} title resonator mode pass = @pass_number ZS�`9r16@b plot/l xrad=.75 �b'�vIX<
g endif ;wZp�lVB7y macro/end Bw��9�O)++ V?-��2F�K] ###初始化变量 D�r"PS�
>. pass_number = 0 # 往返次数初始化为0 # Zv9%�}�%7p field_radius = 1.6 #调整场半径 p<y�\���^a 8v�=t�-GJW c##建立初始单位和高斯场分布 8x�8nQ��*_ array/set 1 128 #设置矩阵为128*128 a�Y �DM)b} units/field 1 field_radius # 定义单位 H|'n|\{�lt wavelength/set 1 10. # 定义波长 c�E�?p~fq< gain/converge/set eps1=.005 eps2=.001 npoints=3 #能量收敛准则的分数变化设置 ]?�NiY:�v� zQ�(��`pld c#调用宏请求最多30个传递,并在收敛条件下退出 #I�J6pg�>K gain/eigenvalue/set 1 R~;8v�1>K� plot/screen/pause 3 6�QN�Z/Ox: TEST = 1 <�S12=<c?' resonator/name conres #设置谐振腔名字 �}�*vE/�W resonator/eigen/test 1 #寻找本征值 A�Xv-%k�}; TEST = 0 R?C�h8mW.! pass_number = 0 #往返次数初始化为0 v"<M�
~9T) clear 1 0 #光束初始化为0 &y-z�[GR[{ noise 1 1 #从噪声开始 ~
cI�`$kJ� resonator/run 30 #宏运行30次 �db>"2�E�E title ex 11: energy per step #设置图形的标题 U��}l=��1B plot/watch ex11a_1.plt #设置图形窗口的名称 oq,�*@5xV2 plot/udata max=0 #设置横坐标范围 v9Lf�|FXo& N37C�Abw�0 ###绘制汇聚场分布 4{0vdpo3F� title ex 11: resonator pass no. @pass_number #设置图形的标题 s=�Kz9�WLy plot/watch ex11a_2.plt #设置图形窗口的名称 MOm+t]v�q1 plot/liso 1 xrad=.75 ns=64 P!{��J28dj obs 1 .3 }n
+MVJ;dG title ex 11: outcoupled beam #设置图形窗口的名称 //bQD�>NBO plot/watch ex11a_3.plt �n�;>���r� plot/liso 1 xrad=.75 ns=64 .Y }k@T40a s~c �cx"HH c##应用透镜并传播到远场 UgOhx-���8 lens/sph 1 100 Un&rP7�0� prop 100 �&��
�sXMB title ex 11: far-field pattern #设置图形窗口的名称,画出远场模式 �c�mY� `$= plot/watch ex11a_4.plt c4bv�Jy��8 plot/liso 1 ns=64 ��Bm6t�f}8 X��G5"��u� c###生成环围功率表 {�5+ 39�=( encircled/calculate/energy 1 .��s|5AC�[ encircled/udata 1 �/s�qfw,h@ title ex 11: encircled energy K1�o&(;l8G plot/watch ex11a_5.plt # ��V8Z@y&ny plot/udata 1 min=0. max=1. # h|<;:o?y�h end �IU"8.(;�o �Z5�`�V\$� Q��"3gvIyc 参考文献 ��6
�tB\X^ C��3
Bo�H& A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). iDl��tN]zS ��}
na@gn� �oqg +�<m� C 谐振腔参数 7=&+0@R#/d ---------------------------------------- 3/]��~#y%2 等效菲涅尔数 0.5 �v`p�@d�jM 放大倍率 2 XQ�tV$�Lw� 腔长 90cm HJ�d{j,�M 孔径1半径 0.3cm �ZQ'�|B� 孔径2半径 0.6cm !�He�QMz�� ----------------------------------------- vTL/%� SJ8 �+k/=L9�#e ## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 Tz�0�XBH_ ## pass_number变量是为了计数宏运行次数,同时作为标题输入参数 z<J2�e^j� ##变量stop用于测试收敛,并将值传递到if语句以退出宏 $)K�Np�dXh ###变量field_radius用于在宏结束后初始化数组并重新调整场半径 a��a�dw#90 variable/dec/int pass_number # 声明pass_number变量为整数 qt4��%=E;[ variable/dec/int STOP TEST # 声明确定收敛的开关 yf�4 i!�~ /Kd'�!lMuz ####定义一个宏,它是一系列命令,通过空腔表示一个循环 (B�v~6tj~J macro/def conres/over # 声明宏conres /新信息覆盖旧信息 0w vA�tK|Q pass_number = pass_number + 1 list #增量计数器 tGS�X�TF}G clap/cir/no 1 .3 # 孔径1 定义 Tl+PRR6D*� mirror rad=180 # 凸面反射镜,曲率半径r=180 ~aXJ5sY"f& prop 90 # 向后传播90cm ��t[A���A= mirror rad=360. # 凹面镜 �q%,y66pFr clap/cir/no 1 .7 # 孔径2定义 �B�A8!NR| prop 90 # 向前传播90cm T�r;&bX5]H variable/set Energy 1 energy # 将光束的能量存在变量Energy h�<n�2pz�} write/screen/on # 写屏 ��y'z9Ya�� udata/set pass_number pass_number Energy-1 #储存光束能量的变化量 �\!%~(�FM gain/converge/test ibeams=1 nstore=STOP # store convergence test in STOP # 8A�u W>7_� gain/eigenvalue/show 1 # 显示本征值 _�lC0XD�Z energy/norm 1 1 #光束能量进行归一化 ^g.H�JQ'vF if STOP macro/exit # 条件退出 ]��L�MtZUz if [!TEST] then #TEST值为0, 执行语句 qc���a=a�} title resonator mode pass = @pass_number ZS�`9r16@b plot/l xrad=.75 �b'�vIX<
g endif ;wZp�lVB7y macro/end Bw��9�O)++ V?-��2F�K] ###初始化变量 D�r"PS�
>. pass_number = 0 # 往返次数初始化为0 # Zv9%�}�%7p field_radius = 1.6 #调整场半径 p<y�\���^a 8v�=t�-GJW c##建立初始单位和高斯场分布 8x�8nQ��*_ array/set 1 128 #设置矩阵为128*128 a�Y �DM)b} units/field 1 field_radius # 定义单位 H|'n|\{�lt wavelength/set 1 10. # 定义波长 c�E�?p~fq< gain/converge/set eps1=.005 eps2=.001 npoints=3 #能量收敛准则的分数变化设置 ]?�NiY:�v� zQ�(��`pld c#调用宏请求最多30个传递,并在收敛条件下退出 #I�J6pg�>K gain/eigenvalue/set 1 R~;8v�1>K� plot/screen/pause 3 6�QN�Z/Ox: TEST = 1 <�S12=<c?' resonator/name conres #设置谐振腔名字 �}�*vE/�W resonator/eigen/test 1 #寻找本征值 A�Xv-%k�}; TEST = 0 R?C�h8mW.! pass_number = 0 #往返次数初始化为0 v"<M�
~9T) clear 1 0 #光束初始化为0 &y-z�[GR[{ noise 1 1 #从噪声开始 ~
cI�`$kJ� resonator/run 30 #宏运行30次 �db>"2�E�E title ex 11: energy per step #设置图形的标题 U��}l=��1B plot/watch ex11a_1.plt #设置图形窗口的名称 oq,�*@5xV2 plot/udata max=0 #设置横坐标范围 v9Lf�|FXo& N37C�Abw�0 ###绘制汇聚场分布 4{0vdpo3F� title ex 11: resonator pass no. @pass_number #设置图形的标题 s=�Kz9�WLy plot/watch ex11a_2.plt #设置图形窗口的名称 MOm+t]v�q1 plot/liso 1 xrad=.75 ns=64 P!{��J28dj obs 1 .3 }n
+MVJ;dG title ex 11: outcoupled beam #设置图形窗口的名称 //bQD�>NBO plot/watch ex11a_3.plt �n�;>���r� plot/liso 1 xrad=.75 ns=64 .Y }k@T40a s~c �cx"HH c##应用透镜并传播到远场 UgOhx-���8 lens/sph 1 100 Un&rP7�0� prop 100 �&��
�sXMB title ex 11: far-field pattern #设置图形窗口的名称,画出远场模式 �c�mY� `$= plot/watch ex11a_4.plt c4bv�Jy��8 plot/liso 1 ns=64 ��Bm6t�f}8 X��G5"��u� c###生成环围功率表 {�5+ 39�=( encircled/calculate/energy 1 .��s|5AC�[ encircled/udata 1 �/s�qfw,h@ title ex 11: encircled energy K1�o&(;l8G plot/watch ex11a_5.plt # ��V8Z@y&ny plot/udata 1 min=0. max=1. # h|<;:o?y�h end �IU"8.(;�o �Z5�`�V\$� 图1.刮刀镜镜前会聚横模 \�[/���}Cy
ojV�N�-*5
图2.单程能量损失图 (�.�b!k�fC 图3 �� J@�J`�)
#(��Yd'qKo 图4.刮刀镜镜后会聚横模 ~N�)(|N��
�@2>�c�e2+ 图5.准直谐振腔的远场分布 V2��g"5nYT
=r&i�`L�{] 图6.使用PIB命令的包围圆能量曲线 6}*4��co��
QQ:2987619807
|