[技术]GLAD：共焦非稳腔模拟仿真 [复制链接]

采用球面反射镜构造了一个共焦非稳腔，该结构与Siegman和Miller描述的结构一致[1]。该谐振腔的准直菲涅尔数和等量菲涅尔数分别为： /_.1f|{B  
#9FY;~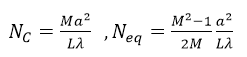  
     (11.1) !aQQq[  
其中，a是孔径半径，L为腔长，λ为波长，M是准直倍率。相应的参数数值为:L=90cm，a=0.3cm，M=2，λ=10μ。带入后计算得：N_c=2，N_eq=0.75。 v3]mZ}W$  
R-lpsvDDL2  
激光在腔中来回一次后，分布的单位是初始时的两倍。要开始另一次来回传输，单位需要缩放到原来的单位，根据Siegman和Miller理论，每个来回损耗大约为44%。 Wd<|DmSy  
fNnX{Wq  
GLAD的计算与该理论相符甚好。 V4>qR{5  
%=EN 3>,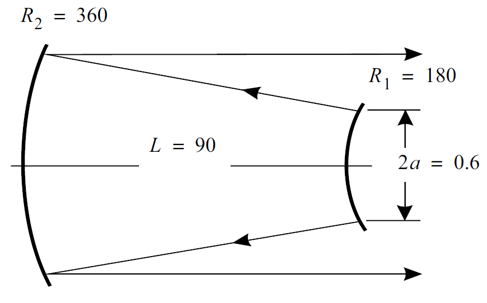  
1Q>D^yPI[  
参考文献 |';oIYs|$  
)E>nr Z  
A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). tX@G`Mr(  
`<x((@#  
[ 30ta<-  
C 谐振腔参数 U1;<NUg  
---------------------------------------- B
t[Wh@  
等效菲涅尔数      0.5 rf=ndjrH  
放大倍率          2 OuuN~yC  
腔长              90cm 8k|&&3_[?  
孔径1半径       0.3cm q-|j =  
孔径2半径      0.6cm L2<IG)oXU  
----------------------------------------- H2 Gj(Nc-  
tS:/:0HnA)  
## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 k=M_2T'  
## pass_number变量是为了计数宏运行次数，同时作为标题输入参数 }K'gjs/N;  
##变量stop用于测试收敛，并将值传递到if语句以退出宏 %
]1.)j
 
###变量field_radius用于在宏结束后初始化数组并重新调整场半径 L=#nnj-  
variable/dec/int pass_number          # 声明pass_number变量为整数 wJMk%N~R:  
variable/dec/int STOP TEST            # 声明确定收敛的开关 &V77WnOY  
OLs<]0H  
####定义一个宏，它是一系列命令，通过空腔表示一个循环 ScCA8JgY  
macro/def conres/over     # 声明宏conres /新信息覆盖旧信息 <TQ,7M4X  
pass_number = pass_number + 1 list #增量计数器 |zCT~#  
clap/cir/no 1 .3                        # 孔径1 定义 DqN<bu2  
mirror rad=180                       # 凸面反射镜，曲率半径r=180 (N[R`LN
  
prop 90                              # 向后传播90cm >Sc/E}3  
mirror rad=360.                        # 凹面镜 AJ"a  
clap/cir/no 1 .7                        # 孔径2定义 tQ7:4._  
prop 90 # 向前传播90cm XT`
2Z=  
variable/set Energy 1 energy           # 将光束的能量存在变量Energy JcJc&cG  
write/screen/on  # 写屏 J{qsCJiB  
udata/set pass_number pass_number Energy-1  #储存光束能量的变化量 ]TX"BH"2  
gain/converge/test ibeams=1 nstore=STOP  # store convergence test in STOP # gUWW}*\ U  
gain/eigenvalue/show 1  # 显示本征值 tQWjNP~  
energy/norm 1 1  #光束能量进行归一化 sEzl4I  
if STOP macro/exit  # 条件退出   oo-O>M#5  
if [!TEST] then  #TEST值为0， 执行语句 qac8zt#2 C  
title resonator mode pass = @pass_number   M7gb3gw6  
plot/l xrad=.75   K'\Jnn  
endif 'dvi@Jx  
macro/end ?mn&b G  
Bk2j|7  
###初始化变量 )\RG NJMC  
pass_number = 0  # 往返次数初始化为0 # U~I y),5  
field_radius = 1.6  #调整场半径 aExt TE  
4H*M^?h\#  
c##建立初始单位和高斯场分布 ?"-1QG  
array/set 1 128  #设置矩阵为128*128 Ou7nk:I@  
units/field 1 field_radius  # 定义单位 >QSlH]M  
wavelength/set 1 10.  # 定义波长 0T
2^$^g  
gain/converge/set eps1=.005 eps2=.001 npoints=3  #能量收敛准则的分数变化设置 6;Sz^W  
AkAQ%)6qV  
c#调用宏请求最多30个传递，并在收敛条件下退出 TD.t)  
gain/eigenvalue/set 1   D5"Xjo*  
plot/screen/pause 3 ~+S,`8-P  
TEST = 1   dJ.up*aR  
resonator/name conres  #设置谐振腔名字 l8H8c &  
resonator/eigen/test 1  #寻找本征值 ^I:f4RWo  
TEST = 0   r)|6H"n#]S  
pass_number = 0  #往返次数初始化为0 ;Z.sK-NJ4  
clear 1 0                                  #光束初始化为0 j.kv!;Rj=  
noise 1 1                                 #从噪声开始 wJF(&P  
resonator/run 30                         #宏运行30次 jp880}  
title ex 11: energy per step                #设置图形的标题 k@P?,r  
plot/watch ex11a_1.plt    #设置图形窗口的名称 M4)Y%EPc  
plot/udata max=0   #设置横坐标范围 b ,e"x48q  
p`)Mk<`dYD  
###绘制汇聚场分布 lS{ ^*(a  
title ex 11: resonator pass no. @pass_number  #设置图形的标题
p735i`8  
plot/watch ex11a_2.plt             #设置图形窗口的名称 'OI(MuSn  
plot/liso 1 xrad=.75 ns=64           e7r3o,!  
obs 1 .3                           >udu~  
title ex 11: outcoupled beam        #设置图形窗口的名称 R5N~%Dg)3  
plot/watch ex11a_3.plt             &G)/i*  
plot/liso 1 xrad=.75 ns=64         W4q |55  
e/b | sl  
c##应用透镜并传播到远场 p]rV\,Yss  
lens/sph 1 100                   ]jSRO30H3<  
prop 100                         G * =>  
title ex 11: far-field pattern  #设置图形窗口的名称,画出远场模式 3}5Ya\x  
plot/watch ex11a_4.plt             *r)dtI*  
plot/liso 1 ns=64                 ,wZq~;2  
0@wXE\s  
c###生成环围功率表 .^8rO,H[  
encircled/calculate/energy 1       #'4Psz  
encircled/udata 1                 sspGB>h8l  
title ex 11: encircled energy       MDCwgNPiQW  
plot/watch ex11a_5.plt # K"cV7U rE  
plot/udata 1 min=0. max=1. # nT9Hw~f<j  
end n(#[[k9&Ic  
)Lg~2]'?j  
J"K(nKXO_?  
=g|5VXW5  
\$!D^%~;  
nh? JiH {