[技术]GLAD：共焦非稳腔模拟仿真 [复制链接]

采用球面反射镜构造了一个共焦非稳腔，该结构与Siegman和Miller描述的结构一致[1]。该谐振腔的准直菲涅尔数和等量菲涅尔数分别为： /Jf.y*;  
\PDd$syDA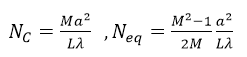  
     (11.1) B`*ZsS=R-  
其中，a是孔径半径，L为腔长，λ为波长，M是准直倍率。相应的参数数值为:L=90cm，a=0.3cm，M=2，λ=10μ。带入后计算得：N<sub>c</sub>=2，N<sub>eq</sub>=0.75。 t@u7RL*n:<  
fVb-$  
激光在腔中来回一次后，分布的单位是初始时的两倍。要开始另一次来回传输，单位需要缩放到原来的单位，根据Siegman和Miller理论，每个来回损耗大约为44%。 x~xa6  
'WaPrCw@Mf  
GLAD的计算与该理论相符甚好。 +fvaUV_-  
l^ZI* z7N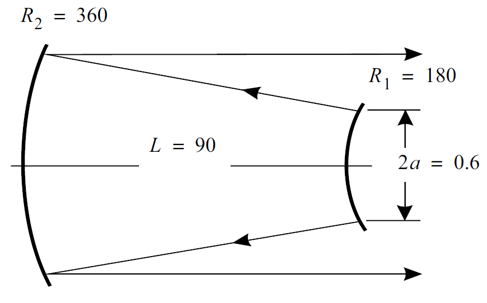  
|f~@8|MQP+  
参考文献 bM8If"  
2gO2jJlv  
A. E. Siegman and H. Y. Miller, “Unstable Optical Resonator Loss Calculations Using Prony Method,” Appl. Opt. Vol. 9, No. 12, p. 2729 (1970). G!K]W:m  
IDnC<MO>  
U2uF&6v  
C 谐振腔参数 |D, +P  
---------------------------------------- 3a.kBzus  
等效菲涅尔数      0.5 wP[t0/dl  
放大倍率          2 fRg`UI4w}  
腔长              90cm ml\4xp,  
孔径1半径       0.3cm Y3Vlp/"rB"  
孔径2半径      0.6cm b Q]/?cCYV  
----------------------------------------- K>*a*[t0Sy  
ylt`*|$  
## ENEGY/GNORM 归一化每一次传递之后的光束能量为分配的值 \ [a%('}  
## pass_number变量是为了计数宏运行次数，同时作为标题输入参数 oc8:r  
##变量stop用于测试收敛，并将值传递到if语句以退出宏 N<QXmgqx  
###变量field_radius用于在宏结束后初始化数组并重新调整场半径 EEGy!bff  
variable/dec/int pass_number          # 声明pass_number变量为整数 %f($*l.  
variable/dec/int STOP TEST            # 声明确定收敛的开关 B}PIRk@a1  
_.L4e^N&UO  
####定义一个宏，它是一系列命令，通过空腔表示一个循环 %Gt.m  
macro/def conres/over     # 声明宏conres /新信息覆盖旧信息 }CeCc0M  
pass_number = pass_number + 1 list #增量计数器 cA%%IL$R  
clap/cir/no 1 .3                        # 孔径1 定义 \Y"W
u  
mirror rad=180                       # 凸面反射镜，曲率半径r=180 ]XI*Wsn  
prop 90                              # 向后传播90cm @)Ofi j  
mirror rad=360.                        # 凹面镜 a4irokJv#  
clap/cir/no 1 .7                        # 孔径2定义 @}u9Rn*d;  
prop 90 # 向前传播90cm **}h&k&%2  
variable/set Energy 1 energy           # 将光束的能量存在变量Energy qUly\b 47  
write/screen/on  # 写屏 9K9DF1SOa  
udata/set pass_number pass_number Energy-1  #储存光束能量的变化量 *Z|y'<s  
gain/converge/test ibeams=1 nstore=STOP  # store convergence test in STOP # .A6(D$O k  
gain/eigenvalue/show 1  # 显示本征值 lo[.&GD  
energy/norm 1 1  #光束能量进行归一化 YW{C} NA  
if STOP macro/exit  # 条件退出   hWX% 66  
if [!TEST] then  #TEST值为0， 执行语句 x
QUu|gtL4  
title resonator mode pass = @pass_number   tKpmm`2  
plot/l xrad=.75   s`0QA!G{-  
endif DZi!aJ  
macro/end 0qX3v<+[6  
\Ym5<];E  
###初始化变量 r#XT3qp$d  
pass_number = 0  # 往返次数初始化为0 # @|\}.M<e*)  
field_radius = 1.6  #调整场半径 :_O%/k1\@  
Uw47LP  
c##建立初始单位和高斯场分布 ^MVkZ{gtre  
array/set 1 128  #设置矩阵为128*128 ih7/}  
units/field 1 field_radius  # 定义单位 l5"OIq  
wavelength/set 1 10.  # 定义波长 6L)%T02C  
gain/converge/set eps1=.005 eps2=.001 npoints=3  #能量收敛准则的分数变化设置 `QXErw  
JU4qzi  
c#调用宏请求最多30个传递，并在收敛条件下退出 U~p
V)J  
gain/eigenvalue/set 1   1Z9qjV%^  
plot/screen/pause 3 %Ah^E$&n2  
TEST = 1   >uSy  
resonator/name conres  #设置谐振腔名字 KQ~i<1&j  
resonator/eigen/test 1  #寻找本征值 ELj\[&U  
TEST = 0   M%@!cW  
pass_number = 0  #往返次数初始化为0 Dc_yM  
clear 1 0                                  #光束初始化为0 E2m8UBS  
noise 1 1                                 #从噪声开始 kkQVNphc  
resonator/run 30                         #宏运行30次 )a-Du$kd  
title ex 11: energy per step                #设置图形的标题 E@ESl0a;  
plot/watch ex11a_1.plt    #设置图形窗口的名称 vvm0t"|\  
plot/udata max=0   #设置横坐标范围 %@u;5qD&  
zRyuq1Zyc,  
###绘制汇聚场分布 *NG+L)g  
title ex 11: resonator pass no. @pass_number  #设置图形的标题 6Udov pl  
plot/watch ex11a_2.plt             #设置图形窗口的名称 \Cii1\R=  
plot/liso 1 xrad=.75 ns=64           UXh9:T'%  
obs 1 .3                           l6d$V9A  
title ex 11: outcoupled beam        #设置图形窗口的名称 ?:)
]h c  
plot/watch ex11a_3.plt             ndkti5L,   
plot/liso 1 xrad=.75 ns=64         ypy68_xyW  
CO`_^7o9(  
c##应用透镜并传播到远场 hC\6- 0u  
lens/sph 1 100                   6Aku1h  
prop 100                         {|'E  
title ex 11: far-field pattern  #设置图形窗口的名称,画出远场模式 :AE&Ny4  
plot/watch ex11a_4.plt             LbkF   
plot/liso 1 ns=64                 ^pYxKU_O  
& 9<+;*/  
c###生成环围功率表 T87m?a$  
encircled/calculate/energy 1       'hs2RSq  
encircled/udata 1                 TTKs3iTXz  
title ex 11: encircled energy       I= &stsH  
plot/watch ex11a_5.plt # *3?'4"B{8  
plot/udata 1 min=0. max=1. # iB498t  
end 4 XAQVq5  
h]TQn
)X]  
H(Z88.OM  
oIduxbAp  
yI"6Da6|y  
dzDqZQY$