-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-03-10
- 在线时间1939小时
-
-
访问TA的空间加好友用道具

|
摘要 d(&���vIjy
��:=��* -x 光栅结构广泛应用于各种光学应用场景,如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM,也称为RCWA),为任意光栅结构的严格分析提供了通用和方便的工具。为此,复杂的一维或二维周期结构可以使用界面和调制介质进行配置,这允许任何类型的光栅形貌进行自由的配置。在此用例中,详细讨论了衍射级次的偏振态的研究。 8<��P.�>u �/c09-�$M�
 �REa�%k��U Z"P{/~H�G� 任务说明 =�%bc;Z�Uu nC z�[#�t �REa�%k��U Z"P{/~H�G� 任务说明 =�%bc;Z�Uu nC z�[#�t 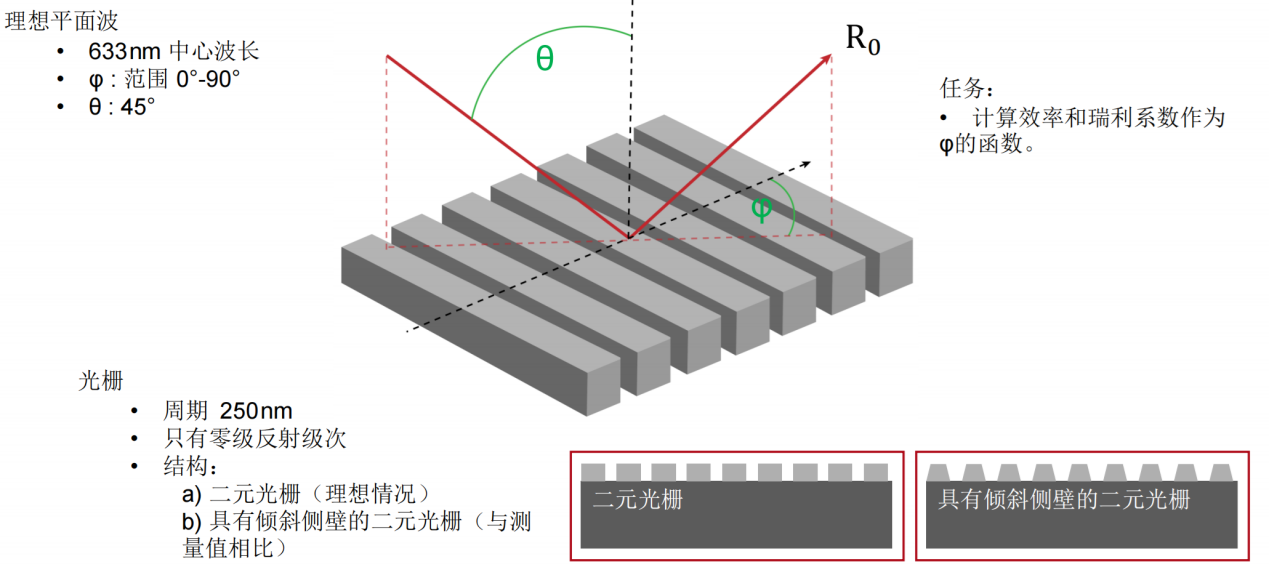 {T$;BoR#O
�Cnc�77EUD 简要介绍衍射效率与偏振理论 z*Fl��ZLHY 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 4>(?R[:�p) 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: "?]5"lNC�| {T$;BoR#O
�Cnc�77EUD 简要介绍衍射效率与偏振理论 z*Fl��ZLHY 某个衍射级次(𝑛)的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的,瑞利系数包含了每个衍射级次(矢量)电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。 4>(?R[:�p) 如果在TE/TM坐标系(CS)中给出瑞利系数,则可以计算衍射效率: "?]5"lNC�| 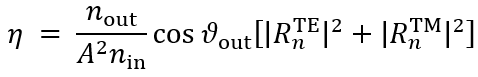 a].Bn#AH!C 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 u*"tZ+|m�� 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: S_�^���"$j a].Bn#AH!C 其中,n_in/n_out为覆盖层和衬底层的折射率,ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外,𝐴表示辐射光的振幅。 u*"tZ+|m�� 如果瑞利系数沿𝑥、𝑦和𝑧给出瑞利系数,则必须应用以下方程: S_�^���"$j 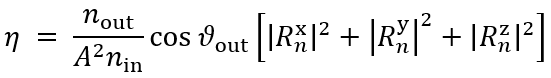 9,,1\�0-T* 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为 9,,1\�0-T* 因此,必须考虑所给出的瑞利系数的坐标系。默认情况下,光栅坐标系中为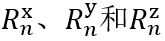 。 %�o~�zsIl� c�4�5�Mv�_ 。 %�o~�zsIl� c�4�5�Mv�_
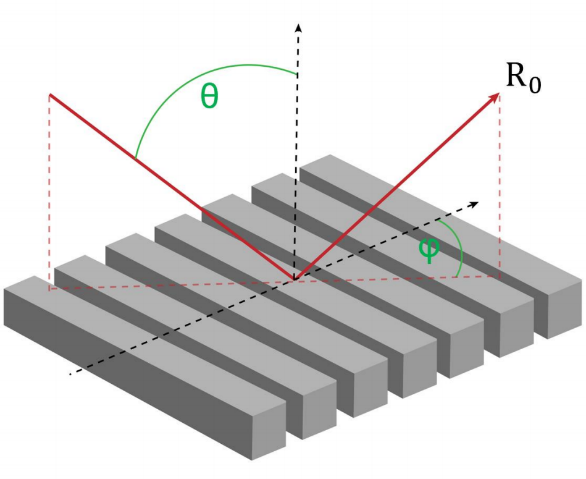
光栅结构参数 �_ TUw�0:& 研究了一种矩形光栅结构。 �@N�O�&3m] 为了简化设置,选择光栅配置,只允许零阶(R_0)反射传播。 3b|�.L
Jz+ 根据上述参数选择以下光栅参数: ^ ���K/B[8 光栅周期:250 nm %e��_WO,R� 填充因子:0.5 !\p�-|�51� 光栅高度:200 nm F
M`�pP��x 材料n_1:熔融石英(来自目录) D�K:d'�zb� 材料n_2:二氧化钛(来自目录) A+?�n=I�Hh VGT�o$R�H 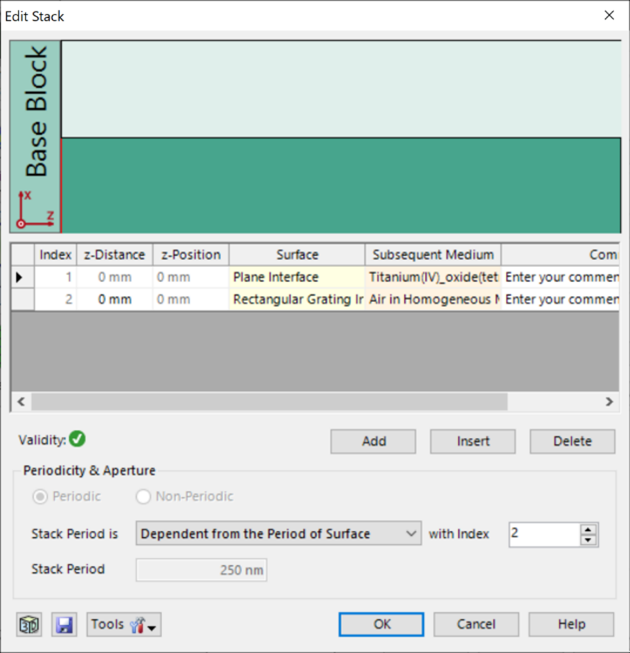 ^y&l!,(A�� j&8�U:�Q�, 偏振态分析 #�*�w$�J�H 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 �E]�Kd`&^} 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 �2-2�'c?% 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 Z$2mVRS`c� SJw0y[IL6( ^y&l!,(A�� j&8�U:�Q�, 偏振态分析 #�*�w$�J�H 现在,用TE偏振光照射光栅,并应用圆锥入射角(𝜑)变量。 �E]�Kd`&^} 如前所述,瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。 �2-2�'c?% 为了接收瑞利系数作为检测器的结果,需要选择光栅级次分析器件中的单个级次输出,并选择所需的系数。 Z$2mVRS`c� SJw0y[IL6( 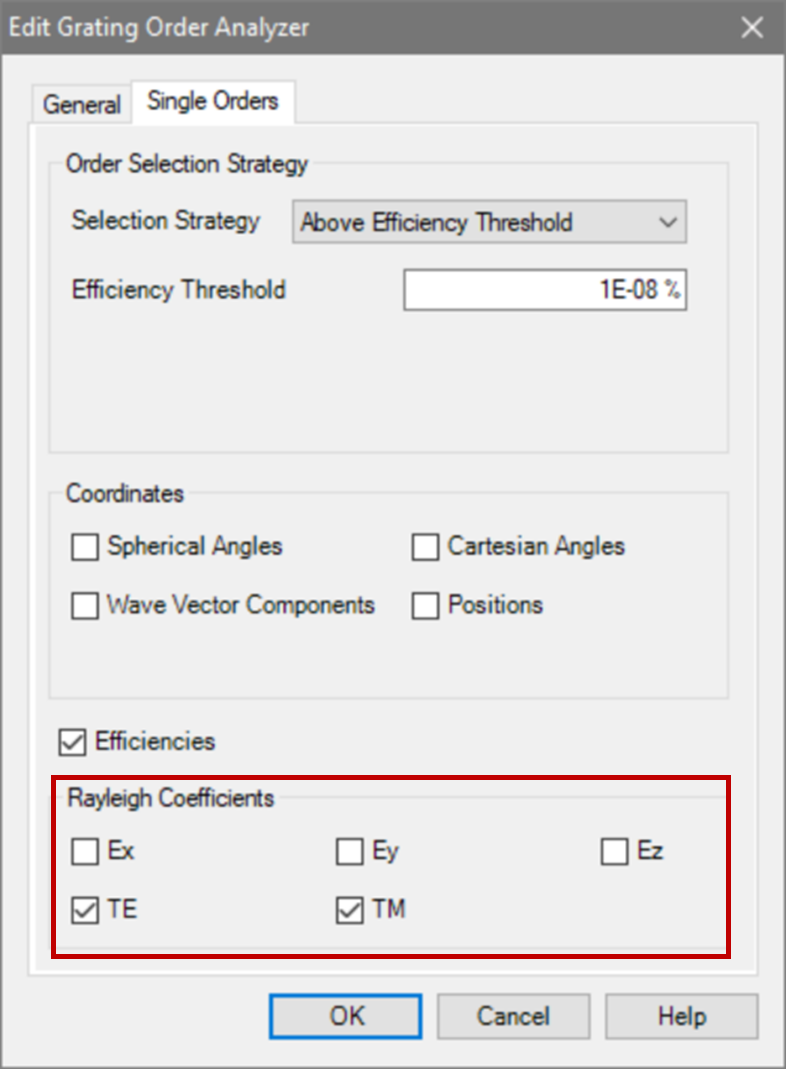 fE7Kv_N-% 2 !{�P�< � 模拟光栅的偏振态 e�nZW2o97c fE7Kv_N-% 2 !{�P�< � 模拟光栅的偏振态 e�nZW2o97c
<�&:3|2��p
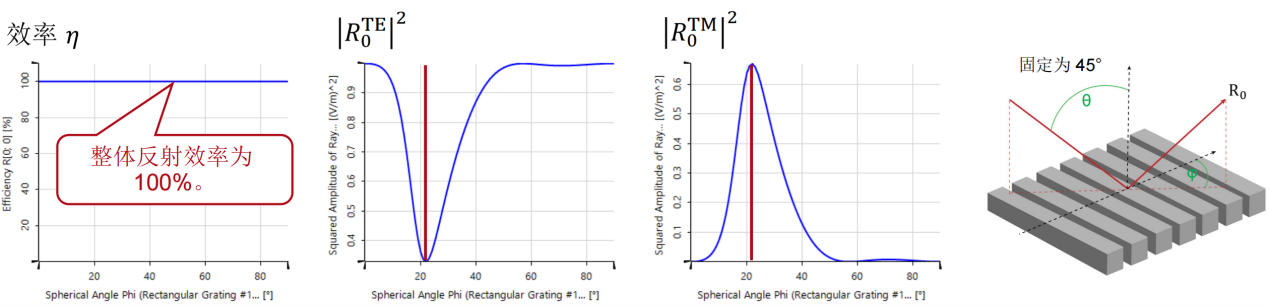 (R�Gl, x�: brZ3T`p+.P 瑞利系数现在提供了偏振态的信息: 7��GK�eq�v 在圆锥入射角为0(𝜑=0)时, (R�Gl, x�: brZ3T`p+.P 瑞利系数现在提供了偏振态的信息: 7��GK�eq�v 在圆锥入射角为0(𝜑=0)时,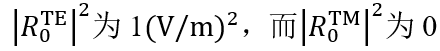 。这说明衍射光是完全偏振的。 {���Ke�3� 对于𝜑=22°, 。这说明衍射光是完全偏振的。 {���Ke�3� 对于𝜑=22°,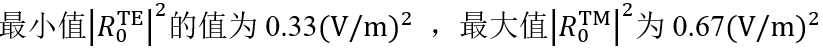 。此时,67%的光是TM偏振的。 ���iTD{��� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 10*�U2FY)] m`�n51�i{U Passilly等人更深入的光栅案例。 I4u'b?*
je Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 S# SA�:>8s 因此,他们将模拟结果与制作样品的测量数据进行了比较。 In�Rn!~�_N 。此时,67%的光是TM偏振的。 ���iTD{��� 对于𝜑>50°,系数接近为常数,因此偏振态也是常数。 10*�U2FY)] m`�n51�i{U Passilly等人更深入的光栅案例。 I4u'b?*
je Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态,以获得不同状态之间的高度转换。 S# SA�:>8s 因此,他们将模拟结果与制作样品的测量数据进行了比较。 In�Rn!~�_N
AX[�/S8|6�
 a]�75z)X�R Y ||���!V 光栅结构参数 �S��x�Mh ' 在本文中,研究了两种不同的制备光栅结构。 jt?R
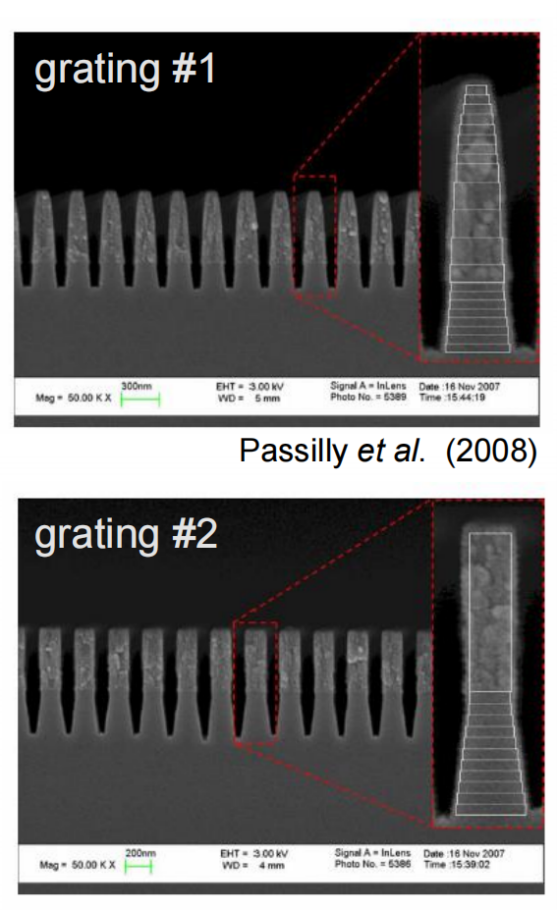
a�1Z� 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 c�pf8f� i� 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 @"Do8p!*(6 但是如果有可用数据,就可以详细分析光栅的复杂形状。 g~N)�~]0�{ a]�75z)X�R Y ||���!V 光栅结构参数 �S��x�Mh ' 在本文中,研究了两种不同的制备光栅结构。 jt?R
a�1Z� 由于加工造成的光栅的理想二元形状的一些偏差是可以预料的,而且确实可以观察到:在基板和侧壁上存在不完全平行的欠刻蚀部分。 c�pf8f� i� 由于缺少关于制作结构的细节,我们将其简化为VirtulLab Fusion中的模拟。 @"Do8p!*(6 但是如果有可用数据,就可以详细分析光栅的复杂形状。 g~N)�~]0�{
 *�_U�
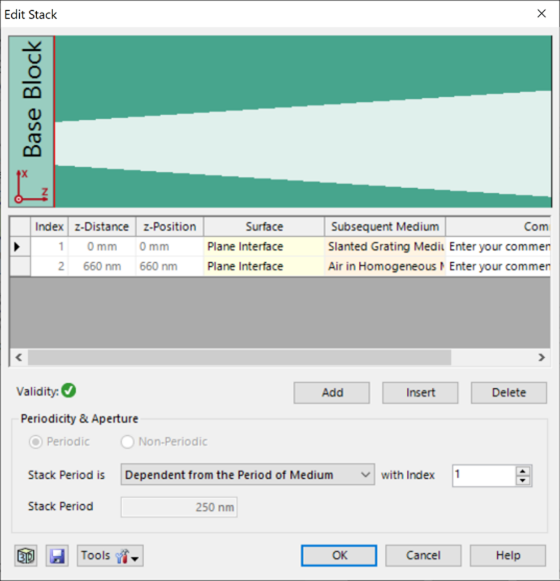
z**M \\)3:1�X�� 光栅#1——参数 �&A��A u:� 假设侧壁倾斜为线性。 t��B�dvk>d 忽略了衬底中的欠刻蚀部分。 -j�<m0XUQ� 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 �g`\Vy4w� 光栅周期:250 nm ��
RtK/bUa 光栅高度:660 nm N\mV+f3A@, 填充因子:0.75(底部) S�rU,-mA W 侧壁角度:±6° {�_�PV~8�u n_1:1.46 cND2(<�jx: n_2:2.08 �6]�na#�<� *�_U�
z**M \\)3:1�X�� 光栅#1——参数 �&A��A u:� 假设侧壁倾斜为线性。 t��B�dvk>d 忽略了衬底中的欠刻蚀部分。 -j�<m0XUQ� 为了实现光栅脊的梯形形状,采用了倾斜光栅介质。 �g`\Vy4w� 光栅周期:250 nm ��
RtK/bUa 光栅高度:660 nm N\mV+f3A@, 填充因子:0.75(底部) S�rU,-mA W 侧壁角度:±6° {�_�PV~8�u n_1:1.46 cND2(<�jx: n_2:2.08 �6]�na#�<�
h�1J��-AfV
 eF!c<
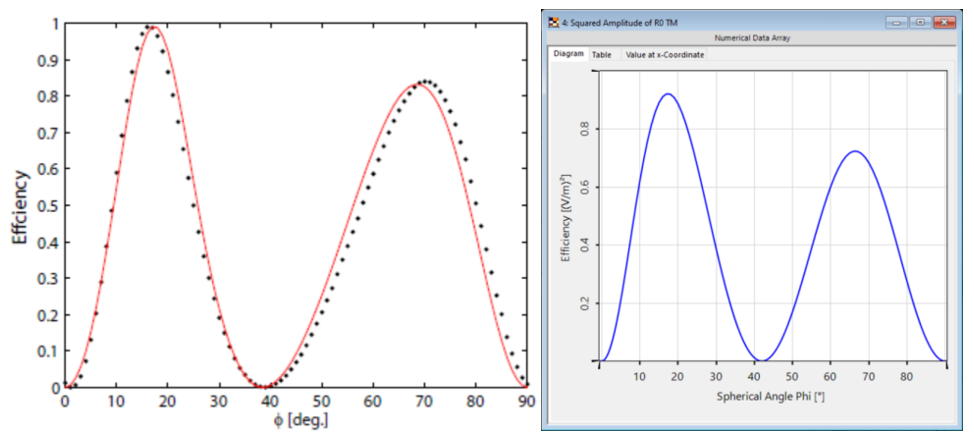
Kc�r UI |D?z<� 光栅#1——结果 h|_G2p^J+" 这两幅图对比之下匹配度很高,特别是图表的趋势。 �e(��j"u;= 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 lYU_uFO�s\ (Z�
sdj�� eF!c<
Kc�r UI |D?z<� 光栅#1——结果 h|_G2p^J+" 这两幅图对比之下匹配度很高,特别是图表的趋势。 �e(��j"u;= 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 lYU_uFO�s\ (Z�
sdj��
 �Onby=Y
o6 =v1s@�5�;~ 光栅#2——参数 $O7>E!u�VD 假设光栅为矩形。 >�L)X�y�q� 忽略了衬底中的欠刻蚀部分。 H<dm��;cU 矩形光栅足以表示这种光栅结构。 �Ci=c"J�dB 光栅周期:250 nm [J��sQ/|=z 光栅高度:490 nm �=OT��w��P 填充因子:0.5 ^2��5�$=�0 n_1:1.46 P�� !6r`d n_2:2.08 )";g�*4�R[ �]'M�Ly�#9 �Onby=Y
o6 =v1s@�5�;~ 光栅#2——参数 $O7>E!u�VD 假设光栅为矩形。 >�L)X�y�q� 忽略了衬底中的欠刻蚀部分。 H<dm��;cU 矩形光栅足以表示这种光栅结构。 �Ci=c"J�dB 光栅周期:250 nm [J��sQ/|=z 光栅高度:490 nm �=OT��w��P 填充因子:0.5 ^2��5�$=�0 n_1:1.46 P�� !6r`d n_2:2.08 )";g�*4�R[ �]'M�Ly�#9 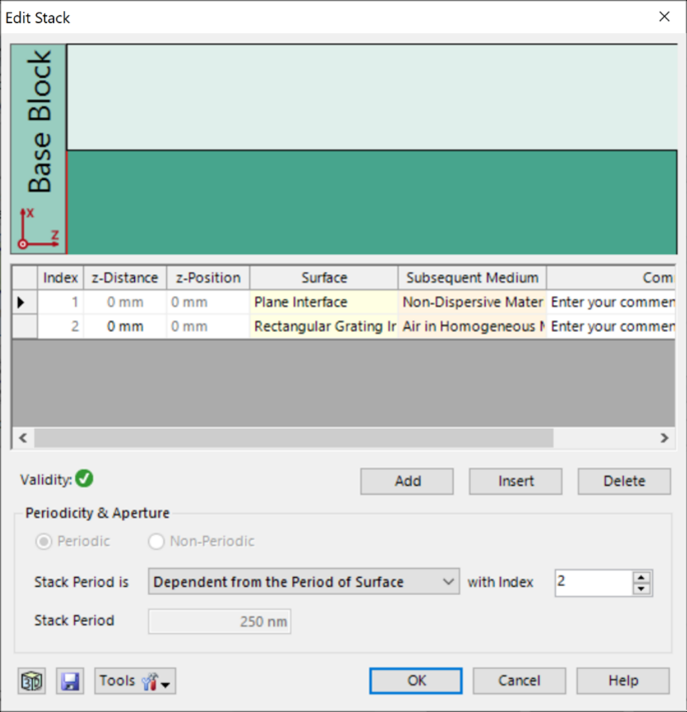 r's4�-�\� Ch^Al��2)= 光栅#2——结果 :@��1�9,.L 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 O zY&^�:>� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 q�48V|6X'q zLC\R�c4� r's4�-�\� Ch^Al��2)= 光栅#2——结果 :@��1�9,.L 这两幅图对比之下再次显示出非常好的匹配度,特别是图表的趋势。 O zY&^�:>� 与参考文献相比,仿真中光栅结构进行了简化,存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据,这种简化是必要的。 q�48V|6X'q zLC\R�c4� 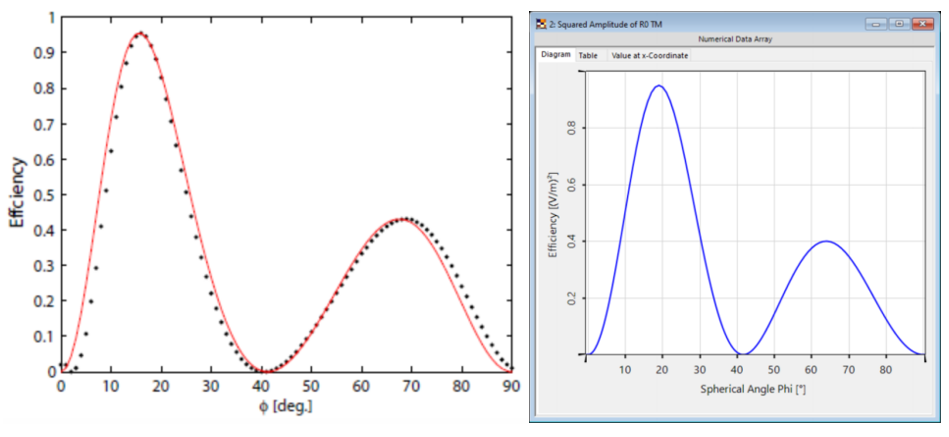 �rn� �U2EL �rn� �U2EL
|