1. 概述 y�Cd-9�zb=
oI0��M%/aM 由于光通信系统向集成化方向发展,因此高折射率对比度以及亚波长尺寸波导的建模变得越来越重要。这些属性需要一个模态求解器,既能够真实地进行几何近似,也可以进行电场的近似。波导尺寸与感兴趣的电磁场区域可能有几个数量级的差别,如长距离等离子体激元。 �*;l��]�8. (|[2J�3ZET 1. 应用 <":;+�N�g+ 硅光子学 R�Y]�#<9>M 波导设计 J���v>gwV{ 空心光纤 :B��y?O"LQ 亚波长光学 6_J$�UBT�� 弯曲波导 j-4VB_��N@ 长距离等离子体激元 *"+=�K,#�D �^s�s��K�� 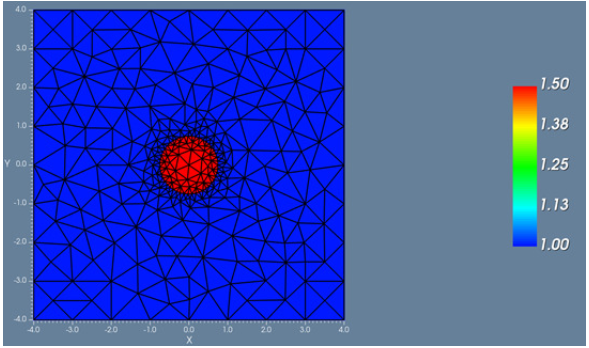 Fu
SL��}�P
Fu
SL��}�P 高折射率对比光纤
h �hG4-�HD �GQ�t8p�[! 图1.VFEM计算的平均误差 V��u)�4dD!
前5个模式误差的平均值如图1中所绘制。其清晰表明,对于一个传播常数,增加基础方程的阶次可以获得更高精度的结果。在x=400时,增加基础方程的级次,等于近乎提高数量级高度的精度。此处应该指出的是,最大平均误差仅为0.3%。 �Y�NLV9.P6 N^#�Z�JoR� 对一个纤芯折射率1.5和包层折射率为1.0的高对比光纤,对比使用不同方法的模态求解器。尽管在SOI波导中可能不算是高对比度,但对于我们来说对比度已足够大了。波导的横截面显示在反面。 )�T�/0S$@�
ge,H-8'Z�� �Z�,RzN5eN 表1:利用多种模态求解器计算的模折射率。包含了模折射率的平均误差。
hU���(umL< 上面的表格显示了对于前六光纤矢量模式计算的模折射率。将一个光纤矢量求解器作为基准,并标签为“Exact”。此外,ADI、FD和FEM求解也都用于计算光纤模态。其中FEM分为两组:第一组使用1阶量,第二组使用3阶量。但在表格中没有给出各求解器所花费时间。其中,FEM计算时间与FD的计算时间大概一致,(FD耗时~109秒,FEM耗时~65秒)。 1�9&�<|qTz udxFz2>_l$ 表格充分说明了FEM模态求解器的优势和ADI的不足。ADI方法计算速度快,但是寻找较高精度高阶模态比较困难,而且其精度随波导对比度提高而降低。FD法优于ADI,但精度最好的是FEM法。这并不仅对于光纤模态,对于矩形和任意形状波导也同样适用。 #D<�C )�Q 7R`M,u~f2^ 有限元求解器如此精确的主要原因之一是其近似几何体的方式。ADI和FD采用小矩形进行折射率采样,这导致了对角线或曲线的阶梯式近似。理论上,矩形晶元可以缩小至阶梯式以进行一个很好的近似,但在实践中它仍然会导致相当大的误差。有限元求解器使用三角形网格可以近似对角线到一个高精度水平,并可以提供足够少的三角来近似曲线。 �$LKI��T0 ~?D4[D|s�B
Te.Y#lCT$ QQ:2987619807 m�`v2:� S}