-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-02-11
- 在线时间1927小时
-
-
访问TA的空间加好友用道具

|
摘要 xG|lmYt76�
USV;j�%U4*
VirtualLab 中的参数耦合功能能够耦合任意光学系统中的每一个参数。不仅如此,这些值可用来重新计算其他参数,因此这个功能也可以创建这些参数之间复杂的关系。例如,如果光学系统的特定参数在变化或优化期间具有固定关系,则参数耦合功能就十分有用。 h�y"�=)�n(
* &� ��: J
 },�,K6*�P� �*�R8P brN 系统参数耦合 �oiItQ4{�< },�,K6*�P� �*�R8P brN 系统参数耦合 �oiItQ4{�<
t8uaNvUM}e
y-_I�Mu.J`
为使用VirtualLab中的参数耦合功能,可通过对于一个光学系统激活”Use Parameter Coupling”。 ;� g�\r��Y
然后,“Edit Parameter Coupling”按钮变为可用。 M�-�A{{q �
通过点击“Edit Parameter Coupling”按钮,出现参数耦合向导。 @gi / 1�cq
=�~'y'�K]� 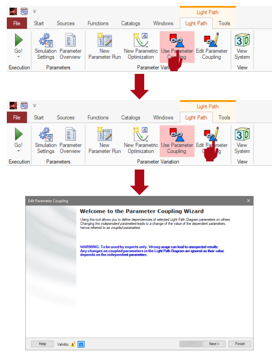 &G_XgQsg{� &G_XgQsg{�
7up�N:7D-� 选择相关的参数 iz2�;x�a�*
L�Dd�g��I 通过点击“Next”,出现如下所示标签,其中包含了当前光学系统的所有参数。 �;M5]XCP�k 请选择所有的耦合参数和必要的计算。例如,选择光栅界面的参数“ZExtension”和“Distance”。 7�o9[cq �w
wj\�k��x\+
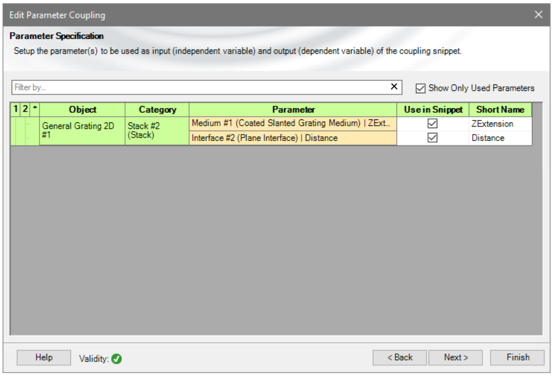 !wIrI/�P7# MZ_dI�"J�, 源代码编辑器 35Fs/Gf-n� 在选择参数之后,必须设置控制耦合的代码片段。 H'jo�3d�~+ 通过点击“Edit”,打开源代码编辑器。 CP�J%<+4%b !wIrI/�P7# MZ_dI�"J�, 源代码编辑器 35Fs/Gf-n� 在选择参数之后,必须设置控制耦合的代码片段。 H'jo�3d�~+ 通过点击“Edit”,打开源代码编辑器。 CP�J%<+4%b
_FzA�f5D�O
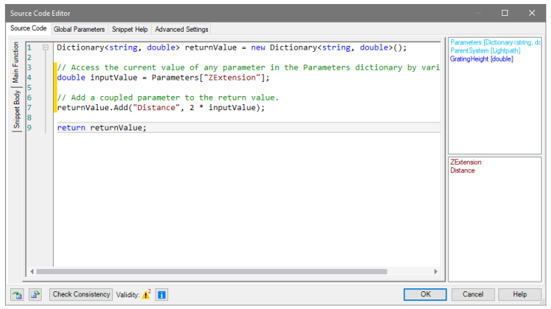
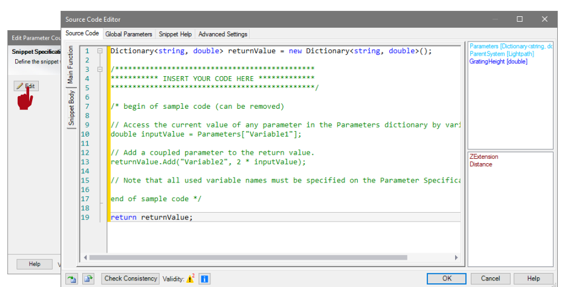 4#ZZw�a]y� 8�i^�d*:R 源代码编辑 �W"H�(HA�� 源代码选项卡包含三个区域: ?{r�-z3@ N −源代码(区域中心)(1) ap�[Q�'=A` −全局变量参数(右上角)(2) �b�E�b+oRI −选择系统参数(右下)(3) {=,�+�;/0� 4#ZZw�a]y� 8�i^�d*:R 源代码编辑 �W"H�(HA�� 源代码选项卡包含三个区域: ?{r�-z3@ N −源代码(区域中心)(1) ap�[Q�'=A` −全局变量参数(右上角)(2) �b�E�b+oRI −选择系统参数(右下)(3) {=,�+�;/0�
p*~b5'+ C+
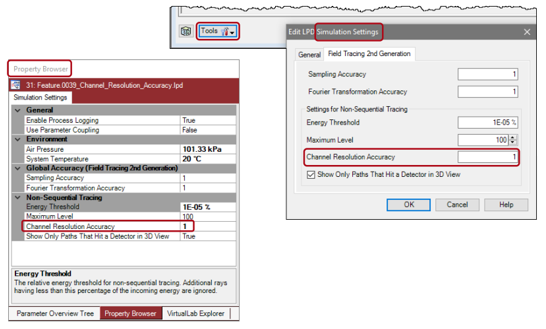 du&9�mO�rr 3e1^r�_�YI 参数耦合的一般实例 BCt>�P?,UO 通常,选择的参数必须从代码库中读取并保存到变量(第4行)。 [q~3$�mjQ� 然后,该值可以作为另一个参数的输出,并进一步计算,例如double(第7行)。 gN�Ss�T�]) du&9�mO�rr 3e1^r�_�YI 参数耦合的一般实例 BCt>�P?,UO 通常,选择的参数必须从代码库中读取并保存到变量(第4行)。 [q~3$�mjQ� 然后,该值可以作为另一个参数的输出,并进一步计算,例如double(第7行)。 gN�Ss�T�])
QVe<Z A8N;
 \8]("l}ms8 F<(?N!C?@� 定义全局坐标系 uOb}R��� � 在这个特定的例子中,定义一个新的全局变量是很有帮助的,它稍后会出现在参数耦合窗口中。 &W
��N
R�{ 这可以在“Global Parameters”选项卡中完成。 ��~;�I'.TW 变量可以显示不同的类型和物理量。 m,r>�E%;Cj \8]("l}ms8 F<(?N!C?@� 定义全局坐标系 uOb}R��� � 在这个特定的例子中,定义一个新的全局变量是很有帮助的,它稍后会出现在参数耦合窗口中。 &W
��N
R�{ 这可以在“Global Parameters”选项卡中完成。 ��~;�I'.TW 变量可以显示不同的类型和物理量。 m,r>�E%;Cj
Gy!��bPVe� 参数耦合的特殊实例 8�)=�"�Ee 在本例中,使用全局变量将其值返回给系统的两个选定参数。 �.|GnT�C q 因此,不需要从字典中读取或重新计算参数。 �0�[1/#�0$ �R�zx�kz��
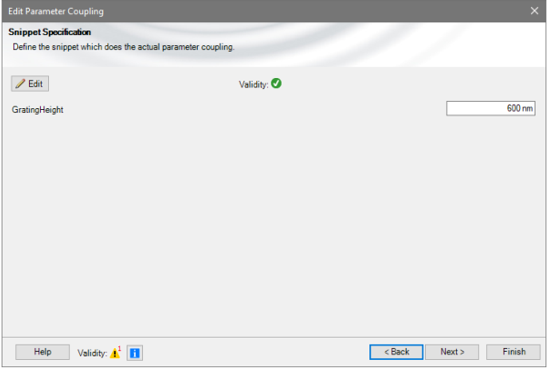
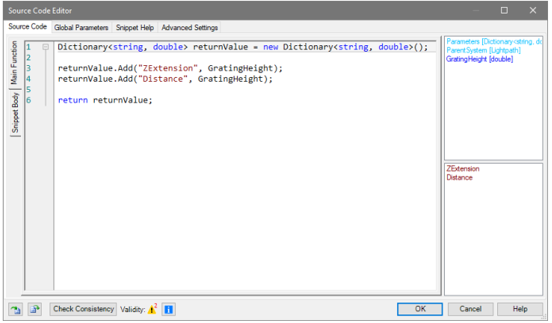 0�f"la�=6� 关闭源代码编辑器后,将出现已定义的全局变量“GratingHeight”。 CFG�(4IM�x 0�f"la�=6� 关闭源代码编辑器后,将出现已定义的全局变量“GratingHeight”。 CFG�(4IM�x
{#&j�����W
 �<4%P�T2�R P���G�A
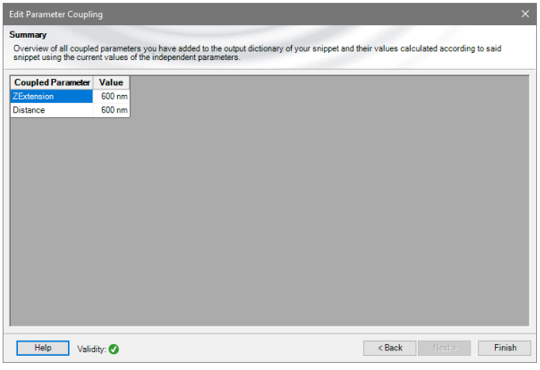
`R 最后检查系统的参数耦合 }P�zHtA,V �<4%P�T2�R P���G�A
`R 最后检查系统的参数耦合 }P�zHtA,V
3j��w4#�GW 在向导的最后一页,可以检查返回的参数和值。 ]%[.��>�mR
�`,�Y/!(:;
 �F*=�}}H�/ 92R�m{n� � 文件和技术信息 |��L~���RC �e�I���+p �F*=�}}H�/ 92R�m{n� � 文件和技术信息 |��L~���RC �e�I���+p  �v��.Xmrry >/�y+;<MZ� �v��.Xmrry >/�y+;<MZ�
:{�~TG]�4M QQ:2987619807 iH)-��8Q��
|