-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2025-12-12
- 在线时间1894小时
-
-
访问TA的空间加好友用道具

|
光束传输系统(BDS.0004 v1.0) ���v"o"W[ f4�7]gtB�- 简述案例 ju{Y6X�J)�
PlzM�`g$A� 光源 ��=#V��^t$
uG�M�z�U&+ - 像散光红外激光二极管 no�xJr/A]� 元件 =� U�H3.�� - 用于准直光束的折射透镜系统 _Hv+2E[�4Z - 生成贝塞尔光束的锥透镜 �eUA]�OF�@ - 聚焦非球面透镜 ��z!"�v�ez 探测器 ~K�w#^.$3T - 点列图 S\).0g�oOW - 聚焦区域的1D和2D研究 U"k�$qZ�[� - 焦深(DOF) P�"�_/��P8 - 光束参数 smf"F\�W�s 模拟/设计 V�%oZ�T>T3 - 光线追迹:初始焦点位置探测 p�"ytt|H�
- 场追迹:计算贝塞尔光束实际的形状和焦深 �A9MM^j�V8 MN�d\)n�X� 系统描述 )�@N ��d3Z
13X�}p�n�W G �tI )O�} 模拟&设计结果 6eV#x%z@v' oF�Wb.�t9< 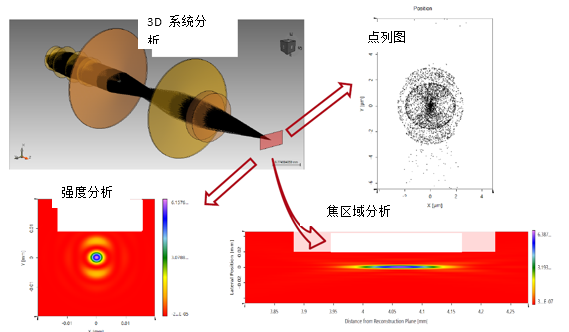 uAn}qr�qE9 uAn}qr�qE9
'�I]XX==_ 在此案例中,你将受益于以下所选的特性: y/Xs+� �{x 焦区域分析: AoS�7B:T;! - 剖面线分析器 e2O6q05 ?Q - 参数运行文件 l�{k_;i�!D - HWxM探测器 HT;^��u"a~ 得到不同有益的信息/说明性的结果等 �h �!^�=
c - 光束质量:光束尺寸和形状 a `R%\�@1� - 焦深 �J�l/w�P�� - 不同2D和3D图样,显示了光束沿着光轴在焦区域传播 �p��u�C�91 �� ��[SPx� 总结 u.�Gn�Xuax �n3�a.)tcC CxF�d/��X,
在这个例子中,它表明了如何通过一对锥透镜来减小焦斑尺寸以及增加焦深,。 F`� U~(>u'
分析贝塞尔光束在焦区域的传播。 Hue�v�D�y4
VirtualLab 能够进行对特殊的元件,如锥透镜生成的光束,能够进行物理光学,如光束的轮廓和聚焦分析。 $v0,�)AL�i
V�zP a�z\e
6z�i>Q?] 1 3Qy@�^��" 详述案例 <Y�]LY_�(
�}�|�Ds�pO 系统参数 u�e_wuZ�i gQn%RPMh�� 案例内容 1�$�>+rW{a
R
BYh�U55B 这个应用案例演示了通过锥透镜对生成“非衍射”(“non-diffractive”)贝塞尔光束以减小焦斑尺寸并增加焦深。 b[74�$W{� �`�z&#�|0O 模拟任务 ;k��<dp�7^ 2�e`�}���O 'R��7� \ 9kL,�6�9d2 C�9�6�/ �� 规格:非准直输入激光光束 K�F.��{��r _ \�D�%��  c[h�~=0UtJ c[h�~=0UtJ 与BDS.0001类似
单模红外二极管激光器光源 ?KC�(WaGJQ �/LD3Bb)O� �3�!CUJs/W
规格:准直透镜和之后的光 ��8�d�c�zC {&�51@��UX BDS.0001中的透镜 l=~!'�1@L}
其后的光束参数 Su��#0�F0 ]~�T�smR[� 规格:锥透镜对 ��9d5�$�cV a1Fx|#!
mq 锥透镜对由两个相同的锥透镜组成。 &h�Oz(825r 张角通常是定义为逆时针。 �da$F��Y�7
�n!jmx��l$
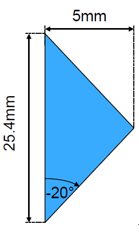 1JJs��Y��X 第二个锥透镜沿光轴放置,并平行于第一个锥透镜,两者的相对距离为20.3672mm。张角为+20°。因此锥透镜对起到类似一个1.0扩束起的作用。 g�m�GK3�am 1JJs��Y��X 第二个锥透镜沿光轴放置,并平行于第一个锥透镜,两者的相对距离为20.3672mm。张角为+20°。因此锥透镜对起到类似一个1.0扩束起的作用。 g�m�GK3�am
N^L�@MR�-
 ��Y}?��8� "��>H�*InF 规格:非球面聚焦透镜 ?
#�K�|l* 从目录的非球面标签下选择一个平凸非球面透镜。 /v{+V/'+� 模型:ALL12-25-S-U(A12-25LPX) �Z
vysLHj� G��Y~$<^AK ��Y}?��8� "��>H�*InF 规格:非球面聚焦透镜 ?
#�K�|l* 从目录的非球面标签下选择一个平凸非球面透镜。 /v{+V/'+� 模型:ALL12-25-S-U(A12-25LPX) �Z
vysLHj� G��Y~$<^AK
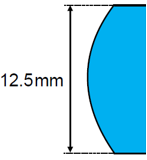 1QoW/X'>. 在BDS.0002中,当波长为1064nm的时候,其后焦距为22.576mm `Q@7�,z=�f 1QoW/X'>. 在BDS.0002中,当波长为1064nm的时候,其后焦距为22.576mm `Q@7�,z=�f
��cAWn�*%
 nS+��Rbhs� UC!�mp? �
详述案例 �|L�2�>|4 3lP;=*�m.� 模拟&结果 �'�/�d�5�1 x�T�HD�_?d 光线追迹:分析光束焦点 �\nl(tU�#j yaUt�DC�.| file used: BDS.0004_OptimizeFocalBeamSize_01_RayTracing.lpd qE��)F�QeN "�5h�k%T�' 场追迹:计算衍射区中的场 �=�?i?-6�M nS+��Rbhs� UC!�mp? �
详述案例 �|L�2�>|4 3lP;=*�m.� 模拟&结果 �'�/�d�5�1 x�T�HD�_?d 光线追迹:分析光束焦点 �\nl(tU�#j yaUt�DC�.| file used: BDS.0004_OptimizeFocalBeamSize_01_RayTracing.lpd qE��)F�QeN "�5h�k%T�' 场追迹:计算衍射区中的场 �=�?i?-6�M
? x)^f+:9| g��Qn��r�. 几何场追迹+(GFT+)引擎在焦区域以为计算光的传输是准确的。 �d� ^bSV4� 实际上,由于几何方法在衍射区域是无效的,则当光束传输受衍射效应影响的时候,必须停止使用GEF+。而在受衍射影响的位置(场重构处)需要使用一种更合适的传输技术。 (,|,�j(=] 使用经典场追迹技术可以将此处的重建光场传播到焦区域(=衍射区)。 oR�V}Nz7hr file used: BDS.0004_OptimizeFocalBeamSize_02_GFT+.lpd `|t,�Uc|7!
�Kd\0�nf�6 场追迹:计算重建平面上的场 ��_7c3=f83
p Cz6�[*kC @C�;1e��7 为了计算衍射区内的场,在离非球面18.5mm处,即几何区域的终结处,使用了几何场追迹虚拟屏探测器。 J�F�=R$!�5 光作用于锥透镜的非连续性顶点会干扰了场数值的重构,因此必须使用一个光阑阻止此效应。 :qzg?�\(� file: BDS.0004_OptimizeFocalBeamSize_02_GFT+.lpd '���/����\ IiYL2JS;t| 使用场追迹计算衍射区域的光传输 �bC{�4�a_B
cO?*(e1m=�
@�Z�5q��2Q
通过经典场追迹,运用获得的重构场以计算衍射区域的光场分布。 w��uq�e{?�
为了实现此目的,生成一个新的LPD,以将重构场放置在存储场元件(Stored Field Component)中。 �W}(A8g#�6
然后可以添加各种元件,如光学组件或探测器,经典场追迹为场提供了更准确的评价。 I68��u%fCv
此LPD可以用于优化和使用自动化工具,例如参数运行(Parameter Run),通过改变到探测器距离来研究光束焦区域。 �w\buQ6pR)
_�"�8�n&=+ file: BDS.0004_OptimizeFocalBeamSize_03_FieldInFocalRegionCFT.lpd o[C^z7WG�0 ��!:(��+�# 在XZ-平面上研究焦区域 �~�D52b�1f
�)V1X�L��� 先前的LPD是用来执行一个参数运行,为了改变焦点和重建平面之间的距离——从3.8mm到4.3mm(对应于从22.3mm和22.8mm之间的一个非球面距离)以来研究焦区域。 CK_�d�Eh2c 两图都显示了焦区域内沿x-轴的光强分布(上图为BDS.004,下图为BDS.002)。 >M<3!?fW�) 相比之下,锥透镜对在XZ-平面提供了一个光束更小的焦点。 �(Y1*�Bs[l file used: BDS.0004_OptimizeFocalBeamSize_04_InvestiateFocalRegion.run }\a#e^-xQ+ |x}Tp�M;ni 在YZ-平面上研究焦区域 ~f<�']�zXv ?�t�/qaUXN 两图都显示了焦区域内沿y-轴的光强分布(上图为BDS.004,下图为BDS.002)。 ����_>gz&� 相比之下,锥透镜对在YZ-平面提供了一个光束更小的焦点。 � 3.&BhL�T file used: BDS.0004_OptimizeFocalBeamSize_04_InvestiateFocalRegion.run 6)I�Nr�,d pc`P;Eu�i� 焦区域内的光束宽度 �$AK
^E�6
%YG?7P�BB� 为了对焦区域的光束进行一个更详细的评估,分别计算了包含(BDS.0004)和不包含(BDS.0002)锥透镜对光学系统焦区域光束的半高宽(HWHM),并使用了高斯TEM00模式进行对比,如下图所示。 Q�'�<AV1�< 通过使用锥透镜对,可以很明显的看出聚焦光斑尺寸和聚焦深度得到了明显的提高。 bZ�owc {!\
!I7$e&�Uz@ file: BDS.0004_OptimizeFocalBeamSize_05_HWHMxyAppEx0002&0004.da Ycr3��$n]e ~N�t�k��-p 理论上,锥透镜产生理想的贝塞尔光束。这些光束有在焦区域内沿着一定的具有距离“非衍射”的特性。 �F^d�J{<yX 因此,与相似光束尺寸高斯光束相比,贝塞尔光束在焦区域内有更高的焦深和较小的发散角。 �+t!]�nE�# 为了对比焦深,将其定义为距离,即束腰(定义为HWHM)与因子√2的乘积。 6-U��_��TV 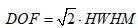 ;d�I�k$_FN 为了比较焦深,计算了高斯TEM00模以作为参考,所有光束的焦面上,其光束束腰与贝塞尔光束束腰类似。 @Q1!x�A^S� 作为对比,计算处的两者的束腰和焦深在下表中列出。 �2?,Jn&i5� 请注意,由于进入锥透镜的光束是一种像差和像散高斯光束,则最终生成的光束不可能是理想贝塞尔光束,。 t3L>@N�W�G 有趣的是,通过使用锥透镜对,光束的像散特性在焦区域得到了明显的提升。这可以在光束y剖面的参数上看出来。 /@��L�k�H$ 此外,相比于有相似束腰的高斯光束,生成的贝塞尔光束的焦深增加了4倍。 ,np=��m�17 �A�R�|�4^� 4D65V�gVDM 透镜后22.576mm处焦斑的强度 I�b(C`4%�� O8�;/oL4 U ;d�I�k$_FN 为了比较焦深,计算了高斯TEM00模以作为参考,所有光束的焦面上,其光束束腰与贝塞尔光束束腰类似。 @Q1!x�A^S� 作为对比,计算处的两者的束腰和焦深在下表中列出。 �2?,Jn&i5� 请注意,由于进入锥透镜的光束是一种像差和像散高斯光束,则最终生成的光束不可能是理想贝塞尔光束,。 t3L>@N�W�G 有趣的是,通过使用锥透镜对,光束的像散特性在焦区域得到了明显的提升。这可以在光束y剖面的参数上看出来。 /@��L�k�H$ 此外,相比于有相似束腰的高斯光束,生成的贝塞尔光束的焦深增加了4倍。 ,np=��m�17 �A�R�|�4^� 4D65V�gVDM 透镜后22.576mm处焦斑的强度 I�b(C`4%�� O8�;/oL4 U file used: BDS.0004_OptimizeFocalBeamSize_03_FieldInFocalRegionCFT.lpd 其他VirtualLab Fusion特征 kowS�| c�#
]E9�iaq6�Z 在此案例中,你将从以下选择的特征中获益 cU;�Bm�}U� 焦区域分析: I;4quFBlMu - 剖面线探测器 C:�E�f6�ZW - 参数运行文件 �E\�iK_'#� - HWxM探测器 -}7$;Q�K&a 得到不同的信息/说明性结果等 �d9{�lj(2P - 光束质量:光束尺寸和形状 1�_Yx]%g< - 焦深 �v
�:pT(0N - 不同2D和3D图样,显示了光束沿着光轴在焦区域传播 }�dc0ZRKgx Ca�-"3aQkc 总结 Gc���O2o�q
>a�"�J);p
`Vvi]>,cg`
此案例显示了通过如何使用锥透镜对来减小聚焦光斑尺寸并增加焦深。 Ejk;�(rx�I
分析了贝塞耳光束在焦区域的传播。 m?S;s�ew@5
VirtualLab 能够进行对特殊的元件,如锥透镜生成的光束,能够进行物理光学,如光束的轮廓和聚焦分析。 fJ�FN��S
y
0�cm3�4\�* 进一步阅读 c���>bns/f jKUEs7�5�] 参考文献 po��z�_=,c [1] D. McGloin, K. Dholakia, “Bessel Beams: diffraction in a new light”, Contemporary Physics, Vol. 4615 – 28, 2005. .}__X�WK5� [2] Frank Wyrowski, Huiying Zhong, Site Zhang, Christian Hellmann, „Approximate solution of Maxwell’s equations by geometrical optics“, Proc. SPIE 9630, Optical Systems Design 2015: Computational Optics, 963009, 2015. �|/,�S��NE
|