-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-01-28
- 在线时间1922小时
-
-
访问TA的空间加好友用道具

|
1.关于公差模拟 7??+8T#�n* • 公差仿真的目的是为了研究制造和对齐公差对一个光学系统性能的影响。 ?qO_t�;:0> • 单参数的公差模拟没有考虑多个不同参数之间的补偿或放大效应对系统性能的影响。 .Q>��.�|mu • VirtualLab Fusion的参数运行文档提供了几种模式,允许对任意数量的参数进行公差分析。 #JWW ;M6F� �Kn?>XXAc 2.参数变化的模式 hDSt6O4�za 为了在公差分析中考虑多个参数,可以使用以下方法: VK[^v;��� • 标准:基于设置的起始值和终止值,所以指定的参数以相同的步数进行线性的变化。 [�K��9l>O� • 编程:该模式允许任意形式的参数变化。 `!K(P- yB? • 扫描:系统性检查并生成所有的参数组合,一般需要耗费大量的计算机内存和时间。 {M��)Y6\�v • 随机:蒙特卡罗模拟,即不同参数的随机组合。如果仅仅进行几次迭代,那么仅能够大概的了解系统的特性。之后可以进行更多次的迭代来得到更有意义的结论。 "fU�=W|lY� @�_J��~zo� 3. VirtualLab Fusion中的公差模拟 &�&n�vv�&a • 上面描述的所有方法都可以由VirtualLab Fusion的参数运行实现。 ~*7�9rDs�{ • 这个案例使用了稍微修改过的案例LBS.001的光束整形器系统,应用单参数和蒙特.卡罗方法来对系统进行公差分析。 C-V,3}=�*2 • !�NuiVC�]� )CD4�k�:bm 4.建模任务 T�u�o`>�ZA %-��/[.DYt 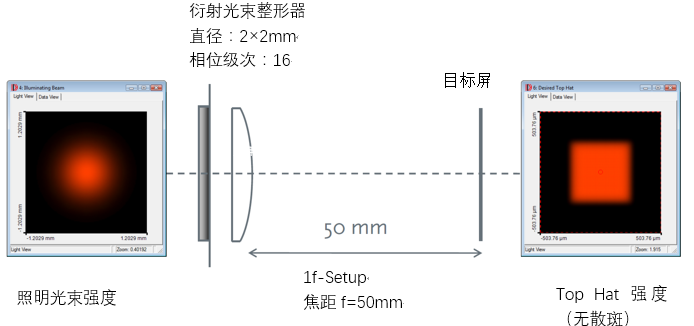 y��
U
=) g �J NPE��yC 分析系统的以下公差: F��w)#[�� _)"-zbh}{ y��
U
=) g �J NPE��yC 分析系统的以下公差: F��w)#[�� _)"-zbh}{
 �zogw1�g&C +v�Ipt{733 5. 模拟对齐公差 &C�pxD."8x nQy.�?�*�X �zogw1�g&C +v�Ipt{733 5. 模拟对齐公差 &C�pxD."8x nQy.�?�*�X 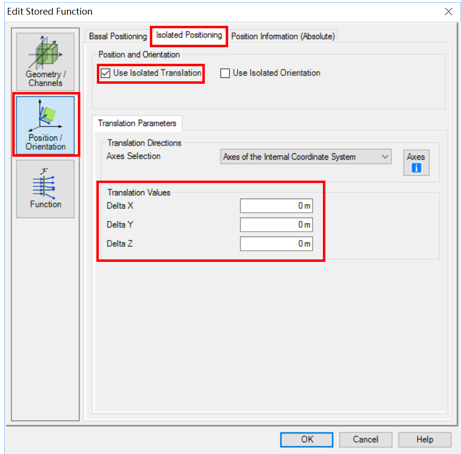 nm`[�\3��R ?\"G�T]�5D J<�'[�P�$D nm`[�\3��R ?\"G�T]�5D J<�'[�P�$D
• 模拟元件的对齐公差必须在Stored Function元件的Position/Orientation标题下选择Isolated Positioning标签并勾选Use Isolated Translation以激活公差分析功能。 Ub2t7M���U
• 公差值由Parameter Run进行改变。在元件对话框中的值可以忽略。 >-*r�tiE��
U�0�� n�SI 6.模拟刻蚀深度公差 2!Y�q9,`�� �]w`)"{j5m
 ikX"f?Q;S2 ikX"f?Q;S2
M�Kf|�(6;~
��O2g9<H��
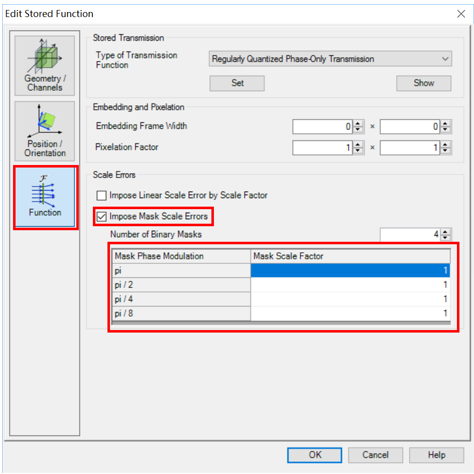
• 模拟掩膜刻蚀深度误差必须在Stored Function元件的Function页面中进行激活。 eyUguA<lK\
• 公差值必须由Parameter Run进行改变。忽略元件对话框中的相关设置。 't.I��YBHx
• 公差值1代表的是理想的刻蚀深度。 w�$�[&ejFb
&kUEnwQ�- 7. 单参数变化 j��)xRzImu ro��fj�&{w 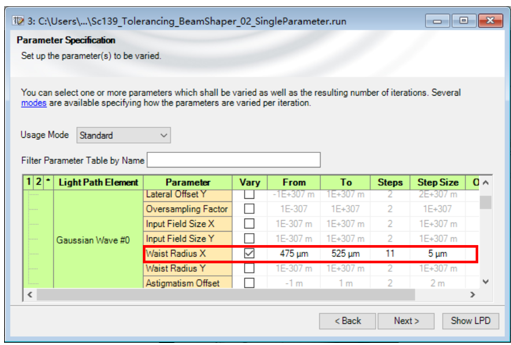 )S@e&�a| )S@e&�a|
Iv��+JEuIi
�]Wr2�I��M
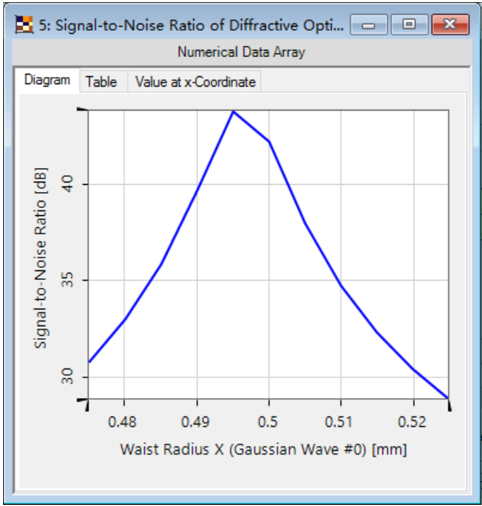
• 激光光束半径对光束整形系统的光学性能有强烈的影响。 IO�3�p&sJ/
• Usage Mode(使用模式):选择Standard(标准)模式以改变单个参数。 �}Z#KPI8\Q
• 选择腰束半径X作为变化的参数。 b�+S�q��[
;)$bhN�FHx
 M15Ce)oB1( M15Ce)oB1(
�)O\w'�|$G
�"jV���:L�
• 光束整形系统对激光光束半径的变化非常的敏感。 7^)8DwAl�
• 信噪比(SNR)将减小到28dB。 ��S52'!WTq
.�8��e]-^Z 8.蒙特卡洛模拟 Q�OiPDu=8z �{*�mf Is 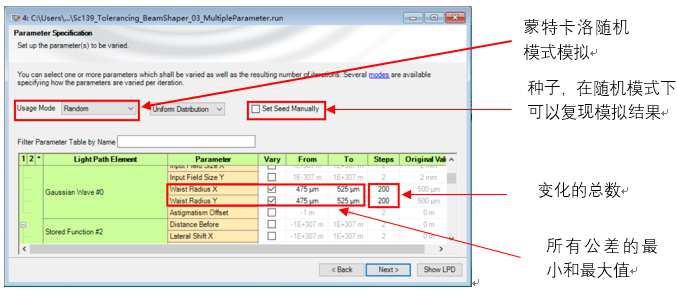 K�CP$i@Pjv G�5*�"P!@6 模拟结果 ��]8@s+��N jV{?.0/�h| K�CP$i@Pjv G�5*�"P!@6 模拟结果 ��]8@s+��N jV{?.0/�h| 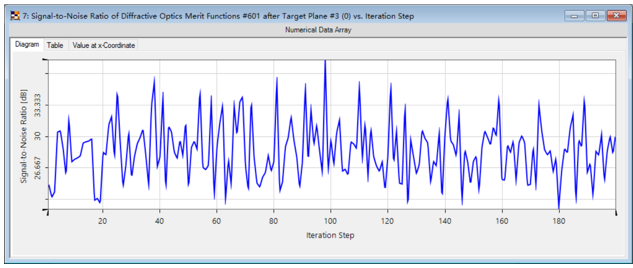 D+#OB|�&Dn D+#OB|�&Dn
6��<1�
2j7
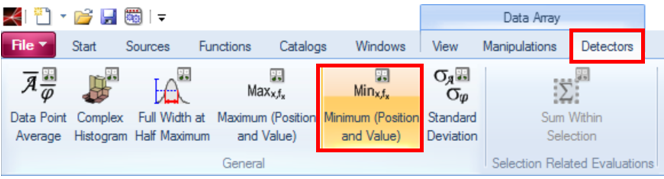 >x�?x3�#SX dhrh "x_?: • 依据于随机参数集的SNR变化。 S��:B$c�>� • 最小SNR可以通过在菜单中点击Detectors-Minimum(Position and Value)探测图蒙特卡罗结果中的最小值以及位置。 �;QO3^P}�� • 最小SNR:22.2dB �c"�KN;9c, • 平均SNR:28.5dB 8u�8�-:c%{ 7[�=\b�L�� 9. 生成的场分布 lC�afs��IB �+�pUG6.j% >x�?x3�#SX dhrh "x_?: • 依据于随机参数集的SNR变化。 S��:B$c�>� • 最小SNR可以通过在菜单中点击Detectors-Minimum(Position and Value)探测图蒙特卡罗结果中的最小值以及位置。 �;QO3^P}�� • 最小SNR:22.2dB �c"�KN;9c, • 平均SNR:28.5dB 8u�8�-:c%{ 7[�=\b�L�� 9. 生成的场分布 lC�afs��IB �+�pUG6.j% 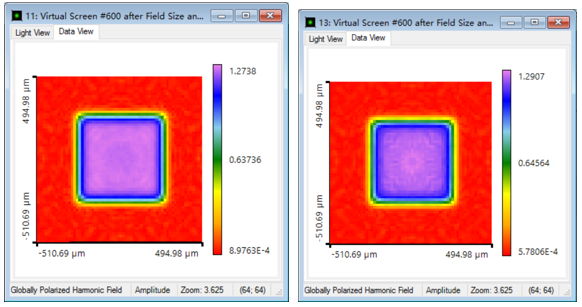 ]31>0yj[�Q • 左图:理想输出强度(SNR38.1dB) Z9�wKjxu+� • 右图:最低信噪比的光图样(SNR22.2dB) 9�K!kU�6Gh • 将蒙特卡洛模拟结果导出到外部软件(例如Microsoft Excel)运行进行进一步统计评价。 d?:KEi-�<7 `PY�=B$?{4 10.结论 \��k�4tYL5 • VirtualLab Fusion支持分析对齐公差和制造公差。 LV2#w_��^I • 参数运行可以运行单参数变化和蒙特卡洛模拟。 RN^<bt{_�U • 蒙特卡洛模拟给出最坏和平均光学性能的概述。 �=csh=V@s� ]31>0yj[�Q • 左图:理想输出强度(SNR38.1dB) Z9�wKjxu+� • 右图:最低信噪比的光图样(SNR22.2dB) 9�K!kU�6Gh • 将蒙特卡洛模拟结果导出到外部软件(例如Microsoft Excel)运行进行进一步统计评价。 d?:KEi-�<7 `PY�=B$?{4 10.结论 \��k�4tYL5 • VirtualLab Fusion支持分析对齐公差和制造公差。 LV2#w_��^I • 参数运行可以运行单参数变化和蒙特卡洛模拟。 RN^<bt{_�U • 蒙特卡洛模拟给出最坏和平均光学性能的概述。 �=csh=V@s�
|