"";[U 在
系统的不同平面上，电磁场分量的傅里叶变换是连接空间域和k域的
物理光学建模中的频繁操作。我们介绍一个场所谓的几何区域，在该区域中傅里叶变换可以在不进行积分的情况下得到，总之是以非常有效的数值方式得到。在几何场域中，场由波前相位控制，因此允许我们将稳定相位的概念应用于傅里叶变换积分，我们将所得到的傅里叶变换算法称为几何傅立叶变换，这项技术被证明是快速物理光学的基础支柱。
FgA'X< wX dt Y 1.光学傅立叶变换 []B9Me yO}RkRA 在物理光学中，我们处理电磁场的六个复数场分量（分别为E和H）。在空间域，他们表示为
1NJ,If] EAiE@r>4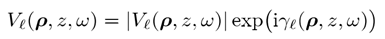 
Fl)p^uUtl !J<}=G5 其中
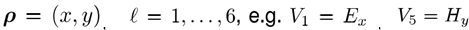
，傅立叶变换到k域定义为
={_.} 
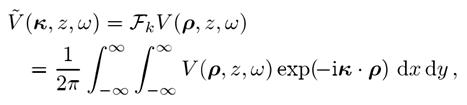
（2）
' *h y!f] 其中，我们使用符号
LvP{"K; *6uZ"4rb.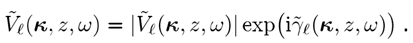 
(3)
Oa7x(wS 9e^HTUFbG 方程2中积分的数值评估需要对a和k域中的场进行取样，我们用N表示采样点的数量，所得的离散傅里叶变换构成了N
2运算。然而快速傅里叶变换（FFT）算法在N中是线性的，这在
原理上使快速物理光学建模成为可能，但FFT需要
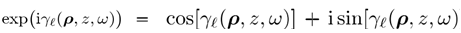
的采样。在光学中，我们通常有强梯度的相位函数，从而导致很大的N值，只有在十分对称的
光学系统中，N才可以很小。因此，尽管FFT在N中是线性的，但是我们很容易在光学上遇到N太大而不能进行快速计算傅里叶变换的问题，这是快速物理光学概念的严重阻碍。
`U:W (\L v,6 为了进一步研究，我们用波前相位Ψ将
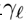
分解（跳过ω）为
Bqo8G-> 9[.vtk\iyH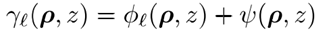 
(4)
yVds2J'w- nT
UKA 对于所有分量都是一样的。 显然，方程 4中的分解是模糊的，其依赖于从源场出发建模中恰当的相位处理方式。由定义
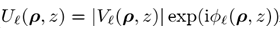
得分解结果
[Y@?l]& o#(z*v@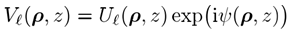 
(5)
m|mY_t } Ej^M~Vv 类似地，我们可以得到
| 0!oSNJ "$)Nd+ny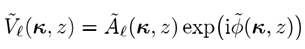 
(6)
nsO! We7~ tkl( 其中波前相位
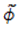
在k域上。应该提到的是，根据方程 5与 在几何光学上是已知的，然后
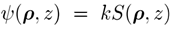
，S为光程函数。我们想强调的是，方程 5的分解在物理光学中是更一般和纯粹的数学方法，我们的目标可以表述如下：我们对不通过采样波前相位因素来进行傅里叶变换的技术十分感兴趣，此时Ψ和
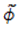
是可通过半解析傅里叶变换实现的二次多项式的形式[1]。这里我们想讨论一个概念，适用于一般的波前相位，但在强波前相位近似，它使用稳定相位的概念。
k&Z3v. p4} ,xQzB 2 几何傅里叶变换理论 N 6CWEIJ 稳定相方法的应用在光学中是众所周知的，例如，用于讨论[2]中的
衍射积分。我们将其用于快速计算方程2的傅里叶变换积分。为此，我们假设除临界点附近以外
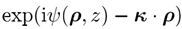
在通过z的平面内具有比U（ρ，z）高得多的空间频率。 根据稳定相位的概念，直接导致基本方程（跳过z )
BLc&q) ;O8Uc&:P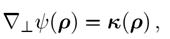 
(7)
j#KL"B_ A kaSi sjd 其中
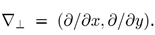
方程7表示k和p之间的映射，我们假设这个映射是开放、双射和连续的，这意味着它构成了一个同胚，这是波前相位 平滑的数学表达式，并确保k域中的结果场可以在非等距网格上插值。在光学中，当场不在苛性区时，通常满足这种条件，稳定相位的概念也揭示出来
aDJ\%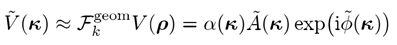 
(8)
c;\} R# 由φ(p)的勒让变换
M9mC\Iz[ 3@ u<Sa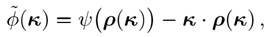 
(9)
jpND" `Q @WcK<Qho 复函数
"zU}]|R HK~uu5j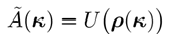 
(10)
?~G D^F R <kh3T 权重因子
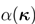
取决于φ(p)的二阶导数，该结果通过将空间域中的场值映射到具有附加权重因子的k域来表示傅里叶变换，其仅作为映射本身而依赖于波前相位。因此，傅里叶变换主要执行场分布的几何畸变，我们称之为几何傅里叶变换。
Vs>/q:I Ie 3
F 我们已经开发了一个数值算法来执行几何傅里叶变换。它利用场的混合采样。相比于函数
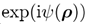
，波前相位φ(p)本身可以通过少量N(φ)的非等距分布值而
参数化。样条插值的节点是可能的候选项。
c e/Z[B+d Koh`|]N 而且，我们必须用等距分布的采样点N(U)来处理函数U(p)的采样。一般来说，我们有
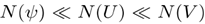
，几何傅里叶变换的数值主要基于 中的线性运算，因此速度非常快；N(U)中U值的智能包也可以快速完成，V的采样可以完全避免。总之，当几何傅立叶变换足够精确时，由此产生的数值算法能够实现非常快速的傅里叶变换，对于强波前相位来说就是这种情况。
jVh I`F{n AGwFD 对于较弱的波前相位，半解析傅里叶变换也适用而快速[1]。连同数值上对于非常弱的波前相位有效的常规FFT，我们获得了一个强大的三元组来处理所有相关傅里叶变换的情况。它在VirtualLab Fusion的第二代技术更新中得以实现，构成了其快速物理光学技术的基础[3]，例如古伊相移就是用这个概念来研究的[4]。
1.+w&Y5
`o7m)T') 3 衍射、几何和远场区域 UzL e#3MU 我们来考虑平面z中的一个场，它可以通过几何傅立叶变换以足够的
精度（由质量
标准来指定）进行变换。那么我们说该平面位于几何区域（GFZ），否则场在其衍射区（DFZ） 。自然地，衍射场区域位于焦点区域附近，而GFZ出现在距焦点区域较远处。如果场进一步传播，则可达到形成几何区域子集的远场区。在几何区域中，我们不限制波前相位 ，这意味着我们也包括
像差。如果几何傅立叶变换为球面的 提供准确的结果，则已经达到远场区域，如表1中概括。对于一个衍射受限场，几何场和远场区是相同的，应该强调的是，在每个平面上，场的区域特征可以通过几何傅里叶变换来研究，这构成了一个纯粹的数学概念。事实证明，在场的几何区域中的物理光学建模可以很快地执行，因为数值上其主要涉及相对较小的波前相位样本数量 。
c ;M7 [y& 表1 场域的定义
dV{N,;z b"`Vn, 参考文献
QBi&Q%p iy [1] Z. Wang, S. Zhang, and F. Wyrowski, "The semi-analytical Fast Fouruer Transform," in Proc. DGaO, vol. 118, p. P2 (2017).
kbij Zj{ [2] J. J. Stamnes, Waves in focal regions. Propagation, diffraction and focusing of light, sound and water waves (Adam Hilger, Bristol and Boston, 1986).
j\V9o 9D [3] Fast physical optics software "Wyrowski VirtualLab Fusion", developed by Wyrowski Photonics UG, distributed by LightTrans GmbH, Jena, Germany.
[3Qu @;"& [4] O. Baladron-Zorita and F. Wyrowski, "The Role of the Gouy Phase Anomaly in the Unification of the Geometric and Physical Models for the Propagation of Focussed Fields, " in Proc. DGaO, vol. 118, p. P3 (2017).
