谐振波导
光栅(RWG)由于其在
波长、相位和
偏振等方面的可调谐性,在研究和工业中有着广泛的应用。RWG的
结构包含一个薄的高
折射率波导
薄膜,该薄膜与光栅接触。波导支持多种导模,并且根据厚度的不同,模式的数量也不同。在这个例子中,我们应用VirtualLab Fusion中的傅立叶模态法(FMM)严格分析RWG的性质。
Q35D7�wo'} SH5a&OVZhn  #/
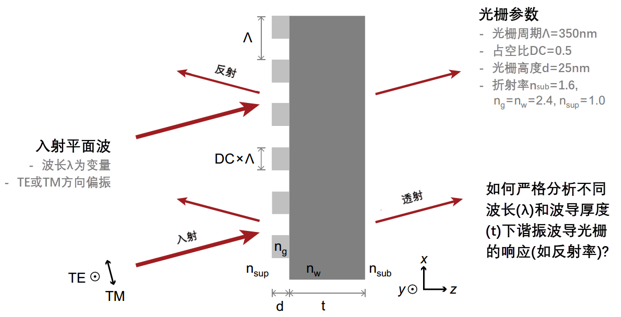
HQ?3h]� j2`%�s��Bo 建模任务 ��s?7"i�E�
#/
HQ?3h]� j2`%�s��Bo 建模任务 ��s?7"i�E�
1�wLEk�p!~
 �s(8e)0Tl r
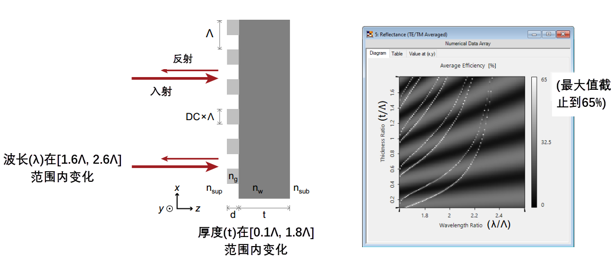
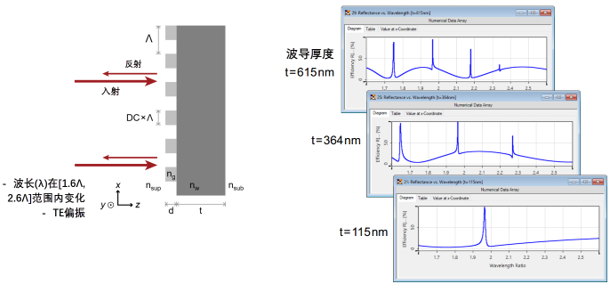
E&}B5PN= 不同波长和厚度的反射率 j58'P �5N
�s(8e)0Tl r
E&}B5PN= 不同波长和厚度的反射率 j58'P �5N
��-+z�8bZ�
 y4N�2gBTKu ZkmY��pi�[ 不同波长和厚度的反射率 '��) �K'Ea ��>����zV� 仿真
y4N�2gBTKu ZkmY��pi�[ 不同波长和厚度的反射率 '��) �K'Ea ��>����zV� 仿真结果来自参考文献:
+GL[ux�e�" G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 a)
1'�!%$���D ^D?{[L�B�c VirtualLab Fusion的仿真结果
�Nz%�Yi?AF 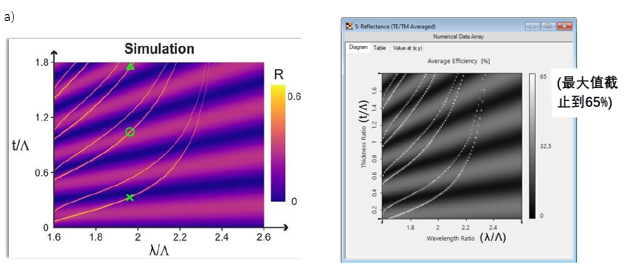 ` 1v�Dp. 特定波导厚度的反射率 7{Z�s"d{s�
` 1v�Dp. 特定波导厚度的反射率 7{Z�s"d{s�
�hi�w>�Q7W
 ;���$g?W�" 4G�'-"u^g� 特定波导厚度的反射率 j_0x�E;g"] X���a���H;
;���$g?W�" 4G�'-"u^g� 特定波导厚度的反射率 j_0x�E;g"] X���a���H; 仿真结果来自参考文献:
giHqc7-PaX G. Quaranta, G. Basset, O. J. F. Martin, and B. Gallinet, Laser & Photonics Reviews 2018, 12, 1800017. [Fig. 3 c)
U�gTgva>? f>�[{1M]n\ VirtualLab Fusion的仿真结果
e�L1�)_M;{ 5�"&=BD�~D 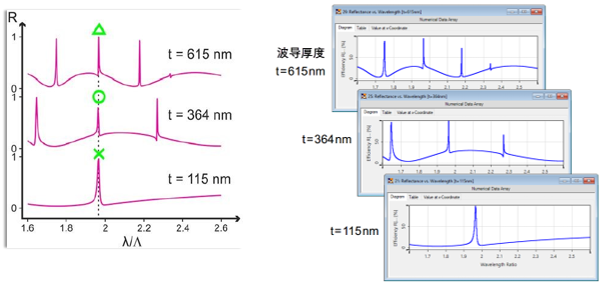 |e91K�miqJ 谐振模式可视化(@λ = 687 nm) 30�b�dcDm, �W=�I~Gh�M
|e91K�miqJ 谐振模式可视化(@λ = 687 nm) 30�b�dcDm, �W=�I~Gh�M 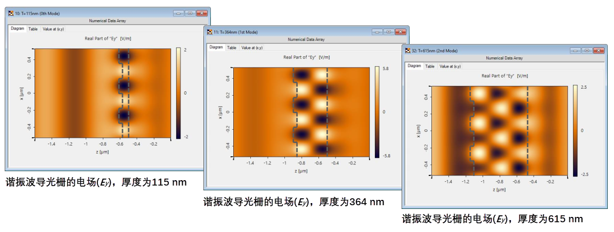 �/kV5~i<1S Y'�Yu1�mH) 角灵敏度分析(t = 364 nm @λ = 632.8 nm) OU[ FiW-�E xm0(U0��
>
�/kV5~i<1S Y'�Yu1�mH) 角灵敏度分析(t = 364 nm @λ = 632.8 nm) OU[ FiW-�E xm0(U0��
>  �8� Y))/]R 3'!*/U�nU� 用聚焦高斯光束检验共振效应 7`S�r�q�I& e3�WEsD�+
�8� Y))/]R 3'!*/U�nU� 用聚焦高斯光束检验共振效应 7`S�r�q�I& e3�WEsD�+ 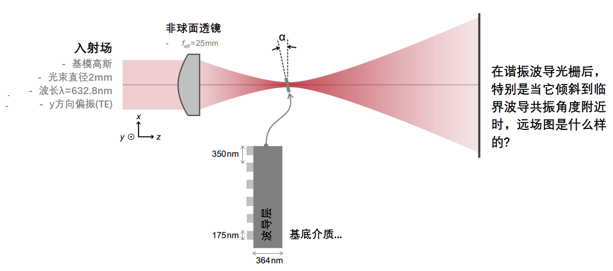 'DD~x�CXE� �;{1��� ws 用聚焦高斯光束检验共振效应 �59H~qE1Md N=��j$~,yG
'DD~x�CXE� �;{1��� ws 用聚焦高斯光束检验共振效应 �59H~qE1Md N=��j$~,yG 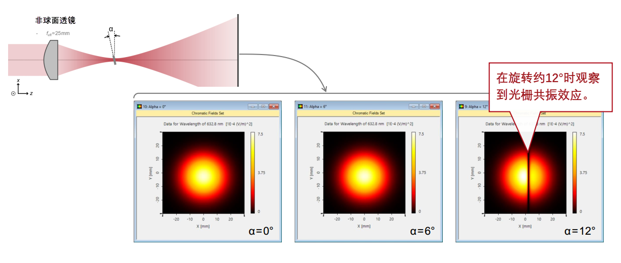 vR�LWs�`1j 6E$ET5p&�l 用聚焦高斯光束检验共振效应 >"�[Nmx0;w 7X8n|NZRH7
vR�LWs�`1j 6E$ET5p&�l 用聚焦高斯光束检验共振效应 >"�[Nmx0;w 7X8n|NZRH7 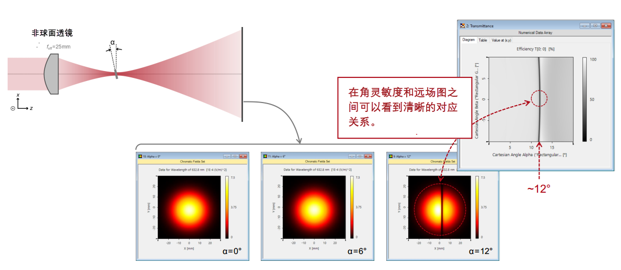 "4L_B�J��Z \�t]_UNGyW 走进VirtualLab Fusion +J3Y}A4W3X
"4L_B�J��Z \�t]_UNGyW 走进VirtualLab Fusion +J3Y}A4W3X
2Y�g\<Ps�N
 `8kL�=%�(h -/R?D1�kOq VirtualLab Fusion的工作流程 N��~%~�Q�� >�/�'/^�h�
`8kL�=%�(h -/R?D1�kOq VirtualLab Fusion的工作流程 N��~%~�Q�� >�/�'/^�h� 构建光栅结构
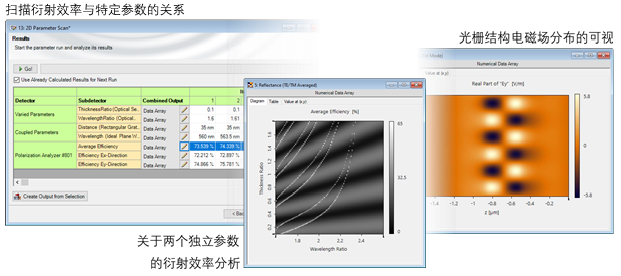
�bd&�N�f2� V�gO.i�n^q ?�:3�rV�fO 分析光栅
衍射效率
hR�,5U=+M7 I\��f\k>;� gT2�k}5d}p 通过
参数运行检查不同参数的影响
a"8H(HAlNn aPin6�L$;) ��{j�%7/T{ 计算光栅结构内的场
>2mV�{i��& �}tbZ[:T{K 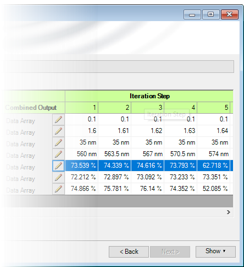 � #zg��"E< �>�g,i"Kg� VirtualLab Fusion技术 .q'�{���3� �SHQ�gI<D7
� #zg��"E< �>�g,i"Kg� VirtualLab Fusion技术 .q'�{���3� �SHQ�gI<D7  :�Fi$��-�g
:�Fi$��-�g