v0t�F�U!Q% 此示例演示了由不同电介质界定的银
薄膜的等离子体激元波导的计算。 该设置遵循 Berini [1] 的举例。 我们主要评论整个计算域上电场强度的数值解,它代表了一个等离子体激元。 但是,对于传播模式项目,也会计算传播常数(传播模式)。
(�n�jTS�+? Q�u7ML]e?z 几何示意图如下:
Qz%q�#4�Zb rd$�T�6�!I 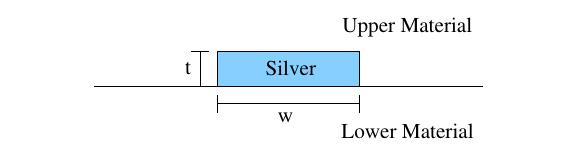 -U?%A:�,a| �NLY���f��
-U?%A:�,a| �NLY���f�� 下层和上层
材料的相对介电常数由
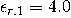
和
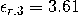
给出。这个金属薄膜的厚度是和宽度是
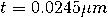
。分析了真空
波长为
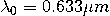
时的
结构。金属薄膜(银)在该波长的相对介电常数为
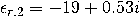
。
JP�
{`�^c� @\x�EK5�SG 在本例中,我们计算具有相对于波导对称平面的镜像对称电场的
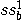
模式 [1]。 因此,只需离散化几何结构的一半就足够了。经过最后一步细化后的三角形几何部分如下图所示。
8x7T��K2r� LTH,�a?l�D  XFl&(I4tB
XFl&(I4tB 由于金属角附近的奇异场行为和几何结构的多尺度结构,等离子体激元模式的精确计算是一个具有挑战性的问题。 等离子体激元的传播主要集中在极薄银带附近。 自适应有限元离散化是解决这类问题的一种方法。 由于角的预细化和自适应细化步骤,网格被细化,特别是在靠近细带和靠近金属角的地方,这些地方的电场表现出奇异的行为,必须非常精确地解决。得到的结果如下图所示:
/6y��Vbo�"