本教程包含以下部分：
O1mK e%'| bY0|N[ g ① 玻璃
光纤中的导光
YUIi; ② 光纤模式
@|%2f@h ③ 单模光纤
D5HZ2cz|a ④ 多模光纤
# Vha7 ⑤ 光纤末端
{Dmjm{
⑥ 光纤接头
6i~WcAs ⑦ 传播损耗
<A'$%`6 m ⑧ 光纤耦合器和分路器
>oe]$r ⑨ 偏振问题
ZJ[
??=Gz ⑩ 光纤的色散
:Z z
'1C ⑪ 光纤的非线性
h2""9aP ! ⑫ 光纤中的超短脉冲和信号
Z/;aT -N ⑬ 附件和工具
9
|vLwQ u-5{U-^_ 这是 Paschotta 博士的无源光纤教程的第 4 部分
d;}nh2* >
"= >3 第四部分：多模光纤
g'qa}/X H+Sz=tg 5 多模光纤是在工作
波长具有多个导模的光纤——有时只有少数（→ 少模光纤），但通常很多。纤芯通常很大——不比整根光纤小多少（见图 1）。
j^2w b+` t1y4 7fX6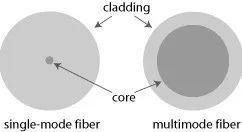 
eHDN\QA 2 图 1： 单模光纤（左）的纤芯与包层相比非常小，而多模光纤（右）的纤芯很大
5N&?KA- *w&Y$8c( 同时，数值孔径往往比较高——例如，0.3。这种组合导致很大的 V 数，进而导致大量的模式。对于具有大 V 的阶跃折射率光纤，在计算两个偏振方向时，可以使用以下公式进行估算：
"!%l/_p?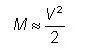 
fx>4 'y3!fN =h 具有较少导模的光纤，例如 V 数在 3 到 10 之间的光纤，有时称为少模光纤。
A=wh@"2 如果需要传输空间相干性差的光，则需要多模光纤。例如，典型的高功率
激光二极管的输出就是这种情况，例如二极管条。尽管它们的输出功率只有很小一部分可以发射到单模光纤中，但对于纤芯足够大和/或 NA 高的多模光纤来说，发射效率非常高。另一个例子是使用发光二极管(
LED ) 代替激光二极管作为光纤链路中的廉价信号源。其他应用存在
成像，例如；图像信息的传输需要具有多种空间模式的设备。
';=O 0)u %n: k# 多模光规格
kq,ucU%>p K&K WN] 多模光纤的基本规格包括多模光纤的芯径和外径。常见的电信光纤（中距离光纤通信用光纤）为50/125 μm 和62.5/125 μm 光纤，芯径分别为50 μm 或62.5 μm，包层直径为125 μm。这种光纤支持数百种导模。 也可以使用具有甚至更大的芯直径（数百微米）的大芯光纤。
5, 6"&vU, fDU !~/# 将光发射到多模光纤中
exUu7& *: X*@dj_, 与单模光纤相比，多模光纤更容易发射光，尤其是在它支持多种导模的情况下。为了高效启动，必须满足两个条件：
EA]U50L( - 输入光基本上应该只照射核心，而不是包层。
- 输入光不应包含大量以大于 arcsin NA 的角度传播的功率。
如果输入光的 M 2 因子足够小，则可以同时满足这两个条件。有效发射具有超高斯轮廓的
光束的最大 M 2因子可以从以下公式估算：
R',rsGd`6j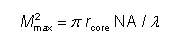 
Ge-vWf-RbB *6DB0X_-} 如果光功率很好地分布在所有模式上，这实际上是来自光纤的近似光束品质因数。（只有当光纤具有许多导模时，估计才准确。）当然，有效的发射不仅需要足够低的 M 2因子，还需要在真实空间和傅里叶空间中具有合适的强度分布形状。
>e [i 5 例如，考虑一根纤芯半径为 25 μm、数值孔径为 0.2 的光纤。图 2 显示了 1000 nm 处的单色输入光束的强度分布，它的数值构造使其刚好充满光纤纤芯，并且其角分布也达到了光纤数值孔径设定的极限。光束轮廓基本上是从具有完全随机相位值（导致巨大发散）的超高斯强度轮廓开始制作的，然后在傅里叶域中使用另一个超高斯函数进行滤波，并再次应用超高斯滤波器在空间域。
VZmLS 4E 角度分布导致复杂的强度变化。对于相同的光束质量，非单色光束的强度分布可能更平滑：虽然每个波长分量都有一个复杂的分布，但这些波动可以平均成一个平滑的整体分布。（特别是对于非单色光束，平滑的强度分布并不表示光束质量高。）
.+A+|yR o= "M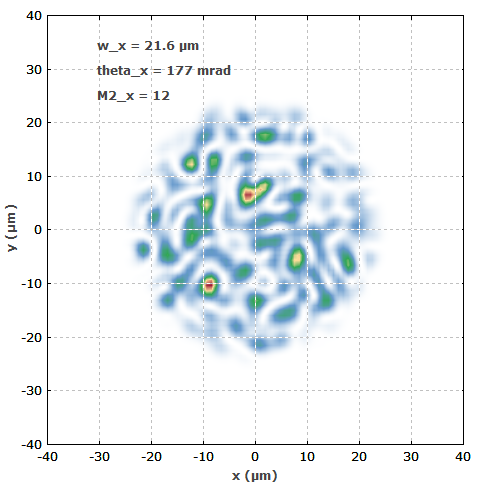 
hp-<2i^"! 图 2： 多模光束 的强度分布，它具有大约最大可能的 M 2值，可有效发射到光纤中。
=mp;.k95 wyO4Y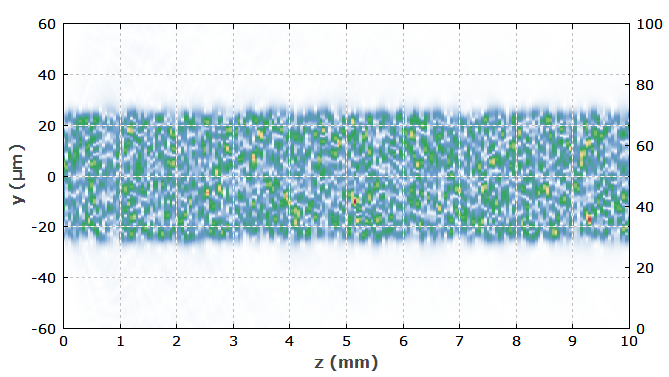 
$6i X 图 3： 光纤中强度分布的演变。在最初的几毫米内，只有很少的光损失到包层中。如果进一步扩大初始光束尺寸或角度范围，类似的
模拟会表现出大量的发射损失。此外，如果光束轮廓大致为高斯而不是超高斯，则有效发射需要稍低的 M 2值（低于 10）。
D!-g&HBTC 如果将光发射到特定的高阶模式，则该光的 M 2值可能比上述公式大 2 倍左右。
X!dYdWw*m 8i#2d1O 输出光束轮廓
)"aV* " .MoU1n{Yc 多模光纤的输出光束轮廓取决于发射条件。此外，它还敏感地取决于整个光纤的条件（弯曲、温度等）。这是因为这种效应会影响所有模式的 β 值，从而影响干扰条件。在较长的光纤长度上，即使 β 值的微小变化也会产生显着影响。
]a*d# 多模光纤有时用于光束均匀化，即获得更平滑的强度分布。但是，这仅适用于多色光，其中不同频率分量的分布平均了。
w HMX=N1/ .Od !0(0 多模光纤中的单模传播
MC.) 2B7 Lh b35;\ 如果将光完全发射到多模光纤的基模中，则光束轮廓原则上应在传播过程中保持不变。然后将获得具有高光束质量的输出，类似于单模光纤的输出。然而，各种干扰可能导致模式耦合：一些光可能会耦合成高阶模式，从而破坏光束质量。
LR.<&m%~. 幸运的是，这种耦合效应通常不是那么强。例如，考虑纤芯直径为 20 μm 且 NA 为 0.1 的阶跃折射率光纤。这是一种少模光纤，支持 6 个导模（计算所有模式方向时）。我们取一段 10 毫米长的光纤并引入一个相对陡峭的弯曲，其中反向弯曲半径在中间平稳上升到 1 / (10 毫米)，然后再次回到零。这种弯曲会导致光纤中间的模式分布发生显着偏移和变形：
#-i>;Rt \B,@ `dw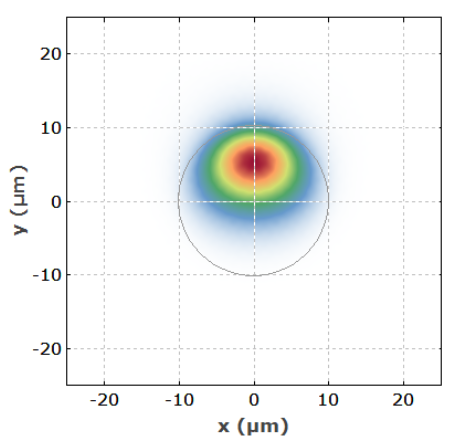 
{d Msz
图 4： 弯曲光纤中间的光束轮廓明显偏离纤芯中心。
9c,'k#k My[ pr_xg 然而，在弯曲结束的光纤末端，原始光束轮廓几乎没有变化。几乎所有功率都保持在 LP 01模式：
Ata:^qI P'[3Fqe 
9} M ?P 图 5： 仅在中间部分弯曲的光纤中光束轮廓的演变。（空间坐标不反映弯曲，它被模拟为折射率分布的线性添加；人们只看到模式分布的偏移作为弯曲的结果。）光束分布很好地回到了原始位置光纤端。
W_(j3pV?Ml ARwD~ Tr 人们可能想知道为什么尽管有很强的弯曲效应，但基本上没有光耦合到高阶模式中。为此，我们需要考虑 LP 01和 LP 11模式的相位常数差异，例如，它高达 4.5 rad/mm。这种相位失配有效地抑制了耦合：在光纤的不同部分，从基模耦合到某些高阶模式的幅度贡献将在很大程度上相互抵消。
"2$fi{9 对于具有大模式面积的光纤，不同模式的 β 值更接近。因此，两种模式的拍长要长得多，即使是相对缓慢变化的扰动也能有效地耦合模式。因此，在大模面积少模光纤中保持单模传播更加困难。
0 e ~JMUb ;m{1 _ 1 渐变射率纤维
f=gW]x7'R+ [H^z-6x:0 对于电信应用，有时希望最小化模间色散，即群速度范围的宽度。这导致电信信号的时间扩展和失真减少，从而允许更高的数据速率。
vJc- 6EO 阶跃折射率纤维在这方面不好。已经发现具有接近抛物线折射率分布的渐变折射率光纤更适合此类应用。图 6 显示了这样一个索引配置文件。
.P%bkD6M x vl #w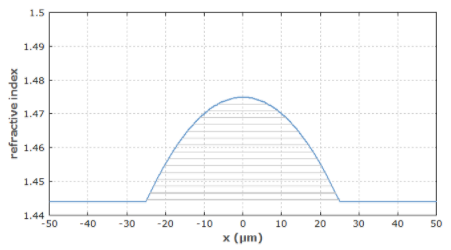 
l=)xo@6 图 6： 渐变折射率光纤的折射率分布，在纤芯区域呈抛物线形。导模的有效折射率（显示为灰线）等距分布。
-g Sa_8R
D_^
nI: 在直观的图片中，人们可能会认为围绕光纤轴振荡的
光线比直接穿过的光线具有更长的路径长度，但这可以通过振荡光线看到的外部区域的较低折射率来补偿。然而，这种含糊不清的想法往往具有很大的误导性。例如，他们可能会产生这样的期望，即具有增加的横向波矢量分量的高阶光纤模式在光纤中经历更大的相位延迟，而事实恰恰相反。因此，我们建议谨慎和怀疑地使用这些想法。
`yXg{lk 图 7 显示了一个模拟，其中高斯输入光束相对于光纤纤芯的中心发生了一定程度的位移。在光纤中，强度分布在没有完全到达纤芯区域边缘的情况下发生振荡。
H-*y h! wX5tp1 ?1J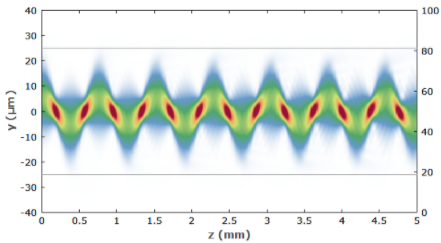 
&L Zn
FR 图 7： 渐变折射率光纤中的光束传播，其中高斯输入光束略微偏离纤芯中心。水平灰线表示核心的边缘。
jaMjZp;{( a PfO$b: 为了比较，图 8 显示了具有相同纤芯半径和最大折射率的阶跃折射率设计。结果看起来完全不同。
(U_ujPD ? (G4at2YLd udUyh%n 图 8： 与图 7 相同，但为步进索引配置文件。图 9 显示了渐变折射率光纤的每个模式的一个点，其中坐标代表模式面积和群速度。可以看出，所有模式的群速度几乎相同，而有效模式区域跨度很大。
~{B7 k: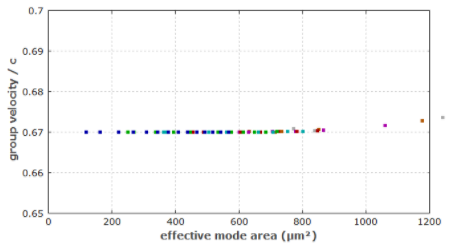 
+tIF
h' 图 9： 具有抛物线折射率分布的渐变折射率光纤的群速度与模式面积的关系。（为简单起见，折射率分布忽略了
材料色散。）不同的颜色表示不同的m值。所有模式的群速度几乎相同。
L<-_1!wh 0c'<3@39k| 下一期将介绍第五部分：光纤末端
l2rd9 -T JNYFD8J~ 敬请关注
