-
UID:317649
-
- 注册时间2020-06-19
- 最后登录2026-01-28
- 在线时间1922小时
-
-
访问TA的空间加好友用道具

|
F$Pp]"82'm 简介 !WKk�=ysFS
���9�81!2* 脚本计算了发光器件与作为发光层实际输出的比例。发光层由厚度为零的层表示,并嵌入在design中代表器件结构。运行开始时,脚本会先确定发光层。 k�i4f*E��j tV�`&�-��H 模型 N/{?7��sG&
hZuYdV{'h� 该物理模型本质上是Jung和Hwangbo [1]提出的,但分析思路有所不同。光由偶极子源产生,并假设由两个相等、传输方向相反的平面波组成,但在光源位置处相位严格相同。 %W�;u��}�` rx:l�KoOnB 定义右手坐标系x、y、z,且z为薄膜表面法向。假设光从放射层中极薄的子层射出,这避免了薄膜横向上的所有相位偏移问题。该子层可能包含数个发光点,以平面谐波的形式输出光,有数种角度分布和某些特定的偏振分布。这样就解决了基本问题,然后考虑其中一个谐波分量。沿着z轴传播的出射波分量的电场为ΔE,假设ΔE为x轴正向。出射可以是正向或负向的。ΔH,对应的磁场就确定了,所以ΔE、ΔH 和出射的传播方向组成了右手系。同时 'Z��[d�7P nFX�AF!,jj
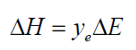 (1) 7%C�It?Z%� (1) 7%C�It?Z%�
zqGYOm�$r� E和H的单位将会归一化使其等同于列矩阵元素B和C。 f�5�?hnt`m L>nO:`��>h 在任一出射介质中都没有入射光,所以计算将从两个介质的输出开始然后返回到有源层和其中的发光子层。在子层中,从任一方向计算的场必须与彼此及发射场连续,这将确定了两个路径的输出量。计算分为正向发射和负向发射,然后将其合并。 D@�hmO]5c� �Ju�J5qIal 发光子层的导纳记为ye,该层的相位厚度为零。多层结构被发光层分为a和b部分,b部分在z轴正方向上。在发光子层中电场用Ba和Bb表示,磁场用Ca和Cb表示,其中B、C和合适的传播方向形成了常用的右手性质。因此Ca为y轴负方向。在a和b区域分别用乘数α和β,并筛选这些乘数以确保连续性条件。在通常的归一化情况下,输出介质中的电场是一致的。在这种情况下,它变为α和β。定义两种逸出介质的导纳为ya和yb。 `Cj,HI�_/* N(�R,8GF5G 对于正向发射,ΔE沿着x轴,ΔH沿着y轴。连续性条件为 ��c!D> {N
WEC-<fN|Y\
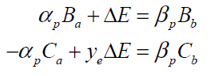 (2) !#.v�yBK#� %�F�S;>;i? 后缀p代表正向。负向发射的ΔE沿着x轴,ΔH沿着y轴负轴。连续性条件为 RndOm.�T�E (2) !#.v�yBK#� %�F�S;>;i? 后缀p代表正向。负向发射的ΔE沿着x轴,ΔH沿着y轴负轴。连续性条件为 RndOm.�T�E
�6B�dyf(t�
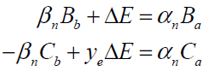 (3) :&$X�e1)i] MVA��c8d�S 后缀n代表负向。该模型是线性的,因此可以通过联立B和C的方程(2)和(3)把场结合起来,得 9p<�:LZ�d~ (3) :&$X�e1)i] MVA��c8d�S 后缀n代表负向。该模型是线性的,因此可以通过联立B和C的方程(2)和(3)把场结合起来,得 9p<�:LZ�d~
�Mf7�E72{D
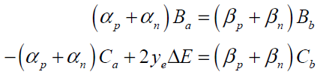 (4) �>4'21�,q� -A���@U0=o 可以写成 I"V3+2��e� (4) �>4'21�,q� -A���@U0=o 可以写成 I"V3+2��e�
�)dg U�mN�
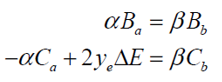 (5) �w4}�(Ab<Y R6P�z#`��n 然后解(5)得α和β。 }}��s)
�+d (5) �w4}�(Ab<Y R6P�z#`��n 然后解(5)得α和β。 }}��s)
�+d
�V'y��xqI?
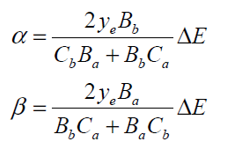 (6) b�V7QVu8� �^�K>p�T}u 输入功率是正向和负向分量的和,为: \[�E���-�: �o}R�|t�Oe (6) b�V7QVu8� �^�K>p�T}u 输入功率是正向和负向分量的和,为: \[�E���-�: �o}R�|t�Oe
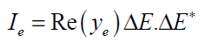 (7) �K�z^��hQd (7) �K�z^��hQd
^z�?=?%��{ (ye一般为实数) 则负向和正向输出为: =0Y'f](2eW z�f")�|9j�
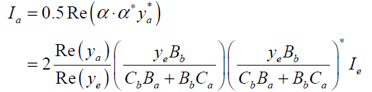 (8) ��.Bijc G (8) ��.Bijc G
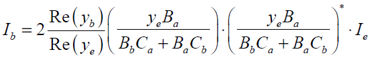 (9) 1��
'�%-y� (9) 1��
'�%-y�
A'v�[SUW'm
5o�a]dc��o 这些结果可直接从薄膜的矩阵表达式推导得到。[1]中结果是从多光束求和得到的,包含了反射相移、透射系数和反射系数,但(8)和(9)与[1]完全一致。 Z{1�6�S=0� m��[�#%�/� 倾斜 �<on)"{W13
���Q
}�8C 以上结果均假设为法向入射。如果引入倾斜入射,所有y被合适的倾斜导纳η替代,可以得到该情况下的结果。离开多层结构的光线将以适当的入射角度传播,可以通过斯涅耳定律计算得到该角度。实际计算的辐照度是垂直于界面的分量。如果分量在横向范围受到限制,那么这些辐照度将转换为总光束功率,无需进一步校正。 �&@Y�oj�%% �[�M2Dy{dh 对话框和输出 x
�k#��*=�
��Cj=J;^vf 一份design文件包含至少一层零厚度层,并指定发光层,必须在脚本运行前打开。如果有不止一层零厚度层,那么最后一层将被选为反射层。遇到问题时请发邮件至support@infotek.com.cn。 �"l��b\�c 图1给出了开始信息对话框。 �#|D:f~"d3 {&b-�}f�"m 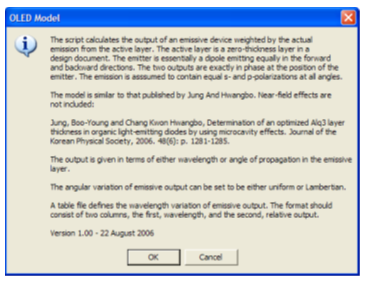 lZ+/\s,]|� 图1. 开始时的说明对话框。 �o}W7.�7^2 Z~B�+*HF� 注意关于角度均匀发射的问题。有两个选项可用,uniform和Lambertian(与cos传播角度值成正比)。这些设置在脚本代码里面。发射输出也可设定为随波长变化,输出分别为波长及对应的辐射输出两列表格。峰值可设为1.0或100,取决于结果是绝对值还是百分比。 ��3�3S`aJ� 4t�(QvIydA 图2给出了一个测试Design。它并不是一个合适的OLED模型。层4厚度为零并且被自动选择为发射层。 ";5�8B}�ki <#!8�?o&i� lZ+/\s,]|� 图1. 开始时的说明对话框。 �o}W7.�7^2 Z~B�+*HF� 注意关于角度均匀发射的问题。有两个选项可用,uniform和Lambertian(与cos传播角度值成正比)。这些设置在脚本代码里面。发射输出也可设定为随波长变化,输出分别为波长及对应的辐射输出两列表格。峰值可设为1.0或100,取决于结果是绝对值还是百分比。 ��3�3S`aJ� 4t�(QvIydA 图2给出了一个测试Design。它并不是一个合适的OLED模型。层4厚度为零并且被自动选择为发射层。 ";5�8B}�ki <#!8�?o&i�
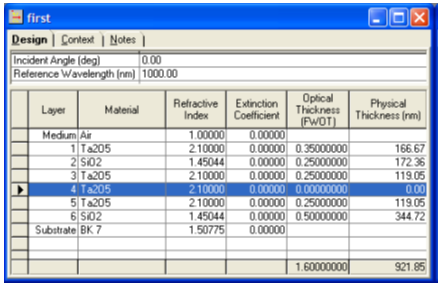 (N9`�Wu�I 图2. 测试design。注意标记层4为发射层。 �gG�D]t;<u _�4A&�%> � (N9`�Wu�I 图2. 测试design。注意标记层4为发射层。 �gG�D]t;<u _�4A&�%> �
 f(W,m
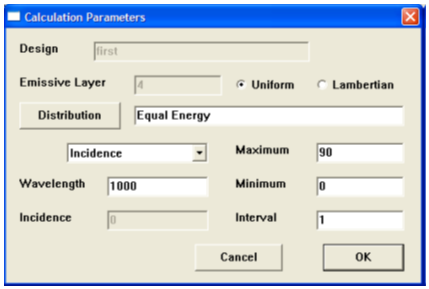
>.;� 图3. 参数对话框给出了入射角度的参数。发射层被正确的识别为层4,该参数不能被编辑。 yl|R�:/2V ,7/�\&X<`B f(W,m
>.;� 图3. 参数对话框给出了入射角度的参数。发射层被正确的识别为层4,该参数不能被编辑。 yl|R�:/2V ,7/�\&X<`B
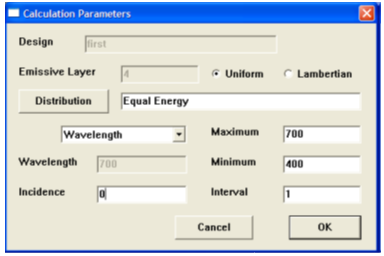 �<C2c"��=b 图4. 参数对话框显示波长作为自变量。 T�&e�%��/ |�Y�g}W�Hm 图3和图4给出了计算参数对话框。Design名字和emissive layer都不可编辑,仅供参考。如果选择了正确的自变量或是脚本的默认值,则相关参数从design文件中读取,它们可在对话框中编辑。点击Distribution按钮会允许一个发射层波长与输出关系的表格以供选择。如果不做选择则默认使用Equal Energy。 (jt*u (C&Y �%��0go%_� 图4给出了波长相关参数。这些数值将用于说明脚本的运行。结果在图5、图6和图7中给出。图中的角度均为与发射材料有关。 HKT{IP+7(L Z�W�`HDrP` �<C2c"��=b 图4. 参数对话框显示波长作为自变量。 T�&e�%��/ |�Y�g}W�Hm 图3和图4给出了计算参数对话框。Design名字和emissive layer都不可编辑,仅供参考。如果选择了正确的自变量或是脚本的默认值,则相关参数从design文件中读取,它们可在对话框中编辑。点击Distribution按钮会允许一个发射层波长与输出关系的表格以供选择。如果不做选择则默认使用Equal Energy。 (jt*u (C&Y �%��0go%_� 图4给出了波长相关参数。这些数值将用于说明脚本的运行。结果在图5、图6和图7中给出。图中的角度均为与发射材料有关。 HKT{IP+7(L Z�W�`HDrP`
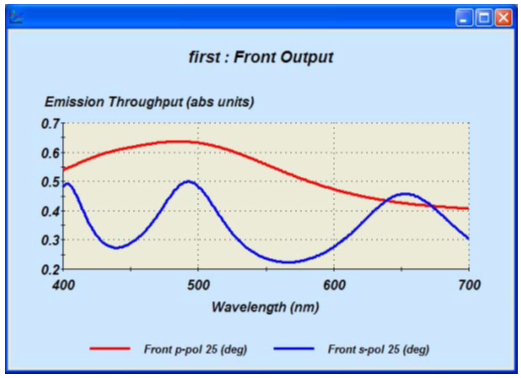 96�k(X��LR 图5. 辐射从器件前表面出射,与从发射层直接出射进行对比。 gS�0,�')�w 7E@$�}&E�� 96�k(X��LR 图5. 辐射从器件前表面出射,与从发射层直接出射进行对比。 gS�0,�')�w 7E@$�}&E��
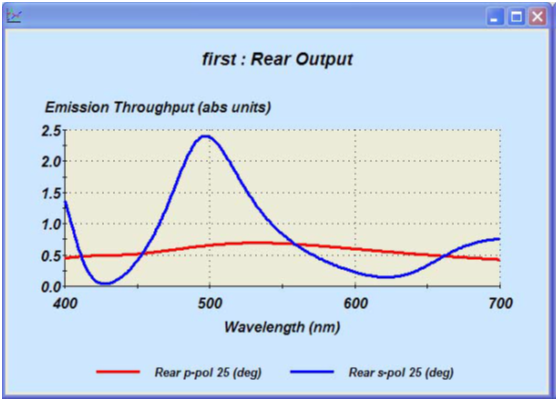 :K5V/-[|V1 图6. 辐射从器件后表面出射,与从发射层直接出射进行对比。 _qd�W�QFuM �HM;���4=% :K5V/-[|V1 图6. 辐射从器件后表面出射,与从发射层直接出射进行对比。 _qd�W�QFuM �HM;���4=%
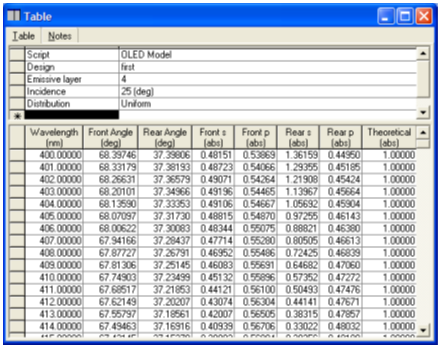 �FkLQBpp(x 图7. 结果表格。front angle是前向介质中出射的光的传播角度。rear angle是后向介质中出射的光的传播角度。theoretical列是从发射材料的输出分布,这里是常数是因为是均匀输出。 :
� �,|=Q} _LL��W�{^V 这个表格显示了出射介质对应的传播角度。front angle是前向介质中出射光的传播角度。rear angle是后向介质中出射光的传播角度。theoretical列是从辐射材料的输出分布,这里是常数,是因为发射材料我们设定为均匀输出。计算参数在上面的表格给出。 J#_\+G i�� !G@V��<�'F 参考文献 LH�1BZ(5�g 1. Jung, Boo-Young and Chang Kwon Hwangbo, Determination of an optimized Alq3 layerthickness in organic light-emitting diodes by using microcavity effects. Journal of theKorean Physical Society, 2006. 48(6): p. 1281-1285. 3�" 8�t)s� ��R�#r��h� 备注 6i5�5J���a qsQ�]M�^@> 如果您的Macleod有Function模块,您可以直接打开该OLED脚本模型。 K4��BTk��! �3�Bu�D/bs �FkLQBpp(x 图7. 结果表格。front angle是前向介质中出射的光的传播角度。rear angle是后向介质中出射的光的传播角度。theoretical列是从发射材料的输出分布,这里是常数是因为是均匀输出。 :
� �,|=Q} _LL��W�{^V 这个表格显示了出射介质对应的传播角度。front angle是前向介质中出射光的传播角度。rear angle是后向介质中出射光的传播角度。theoretical列是从辐射材料的输出分布,这里是常数,是因为发射材料我们设定为均匀输出。计算参数在上面的表格给出。 J#_\+G i�� !G@V��<�'F 参考文献 LH�1BZ(5�g 1. Jung, Boo-Young and Chang Kwon Hwangbo, Determination of an optimized Alq3 layerthickness in organic light-emitting diodes by using microcavity effects. Journal of theKorean Physical Society, 2006. 48(6): p. 1281-1285. 3�" 8�t)s� ��R�#r��h� 备注 6i5�5J���a qsQ�]M�^@> 如果您的Macleod有Function模块,您可以直接打开该OLED脚本模型。 K4��BTk��! �3�Bu�D/bs
kvY}
��yw7 QQ:2987619807 r�< N-�A?a
|