文献作者:Michael Kuhn, Frank Wyrowski, and Christian Hellmann
&P�(vm@�*� 文献来源: Non-sequential Optical Field Tracing. Advanced Finite Element Methods and Applications. Springer Berlin Heidelberg, 2013:257-273.
-hKt�d3WbT :���i]g+</ 摘要 rm!.J�0
�X �Y#f�iJ��� 通过考虑谐波场而非
光线,光场追迹法对光线追迹法进行了概括推广。光场追迹法可以容许位于系统不同子区域的不同的建模技术进行无缝连接。基于分解和互联的理念,这篇文章介绍了非序列场追迹的基本概念,同时推导出了相应的算子方程组和一个求解公式用于仿真。对问题的求值需要局部麦克斯方程的解(分解);并且随着迭代过程的收敛实现解决方案在通过界面处的连续性(互联)。通过使用引入的一种新的光路树算法,对需要求解的局部问题的数量进行
优化。最后,我们展示了一些选择局部麦克斯韦方程组的案例和数值结果。
�x=3+��@'
0hX@�ta[Up 1. 简介 ��p/�?TU 6�gD|QC�~; 现代
光学系统设计需要高级模拟技术。通常,仿真过程中需要在时域或者频域中求解麦克斯韦方程组。即使这些方程的解决方案已经在过去数十年被广泛的讨论,使用比如有限元法(FEM),但由于以下主要原因,其在光学领域仍然非常具有挑战性:(1)感兴趣的波长一般在1微米以下,有时甚至在100纳米之下,(2)一个系统中的长度量级可能在
纳米和米之间变化。应用波长532纳米(绿光)的标准
激光系统,使用特征尺寸仅有几微米的结构界面并且需要在一个系统中与数厘米或者米的结构一同模拟。这表明物理光学模拟,例如,使用标准的有限元法,如今在标准计算机上并不可行。
N�4wMAT:h� 2"B3Q:0he| 另一方面,大部分
光学系统可以通过使用近似的方法,实现足够精确的模拟。尤其是光线追迹方法在光学模拟中得到了广泛的使用。几款基于光线追迹方法的商业工具在二十世纪八十年代随着个人电脑技术的新兴便已确立。然而,光线追迹方法有一些严重的限制,例如,当系统中存在微结构时,其便会失效。
Ts��3(,��Y ,C�jJO�� - 这就是我们引入场追迹的原因[6,12]。场追迹将一个光学系统分解成子域。与光线追迹相比,场追迹是计算通过系统的电磁谐波场。在实际应用中,此方法具有三个基本的优势:(1)场追迹法统一光学建模。其概念允许我们在系统的不同子域中应用任何表述矢量谐波场的技术。(2)应用矢量谐波场作为场追迹的基础,为
光源建模提供了极大的便利性。通过让谐波场集在系统中传输,可以研究部分时间和空间相干光源以及超短脉冲[9]。(3)在系统建模和设计中,探测器函数的任意类型评价非常重要。使用矢量表述谐波场,能够自由的获取所有的场
参数,因此能够引入和评估任意类型的探测器。在场追迹中,通过求解局部麦克斯韦问题以计算各子域。这些局部问题具有这样的属性:能够在所有容许函数的子空间中产生解。此外,近似的麦克斯韦求解器足够精确且比严格的麦克斯韦求解器更高效。从这个意义上来说,我们调整了“域分解以及分解和互联”方法的主要理论,而这些方法已经被使用在许多应用中,参考引用文献[3]和[4]。场追迹的目标是通过联合不同的子域求解器,在保证计算精度的情况下,尽可能快的构筑出一个针对问题的求解器。通过施加连续条件,将局部解进行耦合以求解全局问题。为了这个目的,我们希望将那些在光学中已经完善建立的追迹技术普遍化。文献[12]着重介绍了序列情况。此处我们希望将此理论扩展到非序列情况中并增加更多的描述求解器的算法模块。这篇文章展示了如何进行将分解和互联进行应用。
vA�#?\j�2� 这篇文章结构如下。在第二部分,我们讨论了局部麦克斯韦求解器的定义。我们描述了如何使用分解和互联的方法来阐述3D麦克斯韦问题。基于诺依曼级数推导出来的使用局部算子的解公式导致一个无穷求和。通过使用一个修订的公式,可以将求和作为一个迭代过程进行重构,这个公式将在第三部分讨论。算法本身可以归结为一个光路逻辑树。应用场追迹方法求解局部问题将在第四部分讨论。最后,我们将在第五部分呈现数值结果并在第六部分进行总结。
&:��Sb�$+z f�c9gi4y9� z<s4-GJ)�? 2.分解和互联方法 B�k8 '*O/) `�*Jw[Bnh8 光学系统建模主要是求解麦克斯韦方程组以在R
3中获得电场E和磁场H。麦克斯韦方程组的频域表示如下
�FUKE.Ux�d 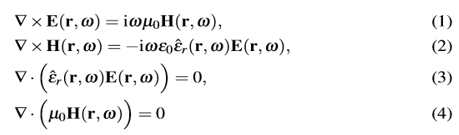 Wg5i#6y8w� `�L?9-)m<f
Wg5i#6y8w� `�L?9-)m<f 对于线性物质方程和各向同性介质。系统的折射率n ̂(r)是非均匀的,并且定义如下:
�Q)Zk�UmW� ai~JY����[ 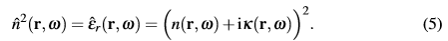 G+l9�Qa�Fv
G+l9�Qa�Fv ,其中r=(x,y,z)。各频谱w的解是一个电磁谐波场,它是由三个电场分量和三个磁场分量决定的。在光学系统建模中,求解系统域Ω中所有场的分量是一个最普遍待解决的任务。
�A�V?<D.<� 为了简化符号我们使用场矢量V来概述六个场方向:
Y\ G�^W8�� 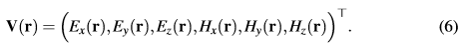 TkV$h(#!f& Ia>>��b #h k<\]�={�|=
TkV$h(#!f& Ia>>��b #h k<\]�={�|= 由麦克斯韦方程来看,很明显六个场方向并不是独立的。尤其是我们总是可以从电场矢量计算出磁场。然而我们使用场矢量V是为了强调模拟中必须包含了六个场分量,这为我们定义探测器提供了最大的灵活性,能够方便的让我们进行光场性能评估。例如,在能量考虑方面,坡印廷矢量是非常实用的。其定义结合了磁场和电场。
^1NtvQe@Y\ IP�+1 ��:M 图1阐述了所关心的建模情景。系统位于域Ω⊂R
3中。J 个子域Ωj都处在折射率n ̂(r)中,其中r=(x,y,z)是非均匀的。我们使用Γj来表示各子域Ωj的边界。
h�}$]3/5�H -~�ycr[}x 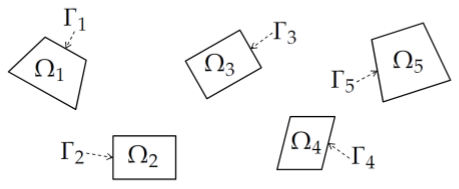 /'�0,c�Jnm IXmO�1*o@�
/'�0,c�Jnm IXmO�1*o@� 图1.形式上一个系统被分成J个子域Ωj。所有的子域都处在一个折射率为n的均匀和各项同性介质中。子域的边界用Γj表示。
M)!:o/!c�S o*1t)�HL�< 0��!,)7��� 从实际的角度来看,子域与系统的元件紧密相关,但对于接下来要讨论的内容来说那并不重要。特别是其有利于将一个元件分解成多个子域。此外,有时候这有利于在系统的均质区域定义一个子域。根据建模技术的规格,可以在一定程度上自由地选择子域的形状和尺寸。所有的子域都处在折射率为n的均匀电介质中。
P��;�!4 VK #�L�,5;R{` 为了获得一个公式以模拟整个系统,我们应用了一些分解和互联的方法。首先我们为每个子域Ωj定义了散射问题。然后我们确定方程以将局部散射问题的解进行互联。最终,全局问题由一个均衡方程描述以确保场的连续性。
d<l�-Ldle 为了定义局部散射问题,我们将边界Γj处的光场表示为
Y/w��) V�V 2���-M]!x) UT�7�"�.1H  IWcYa.�=tZ
IWcYa.�=tZ 此外,我们使用
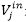
来定义作用于子域Ωj的输入光场,使用
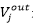
来定义对应的输出光场。通过算符
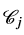
散射问题的解定义了输入场到输出场的映射
7w=�%aW��| ;j/-�ndd&&  yD!V;?EnK� �P��=9Z�m
yD!V;?EnK� �P��=9Z�m 互联问题描述了在均质中一个输入场和一个输出场中任意一对(
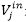
,
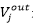
)之间的关系。为此我们引入了算子
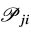
,将输出场子域ⅈ映射到输入场子域j,其中ⅈ≠j:
�^#L?�HIM �t#h<'?\E 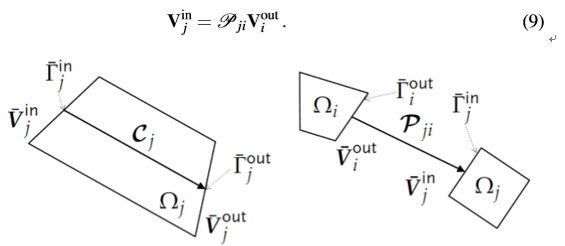
图2.场追迹
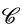
经过边界Γj(左边)的两个平面部分之间的一个子域和场追迹在两个子域(右边)的平面边界部分间的传播
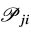
的应用示意图。
'zhw]L;'g� _;+N=/l��0 6axm��H~�_ 以前计算
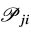
需要求解一个麦克斯韦问题,但是现在在均匀介质R
3的半空间(与Γj相关)且在边界Γj处的入射场为
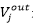
时,在边界Γi处所求得的解仅产生
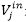
。
Wy%�F���
� E5� ��0$y: 最后,我们必须确保光场的连续性。由此引出处理所有子域间的多次作用问题的均衡方程。在Γj处的输出场必须满足方程
N:@C%
UW} #U�H7�z 4u 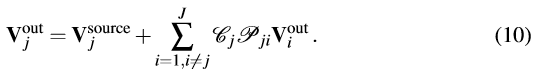 ��'3@WF2a d/�OIc){tD <�~Tl�x��:
��'3@WF2a d/�OIc){tD <�~Tl�x��: 可选的光源场
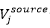
会作用于子域j的输出场,并因此和包含所有其他子域贡献的和相加。根据(10)我们推导出一系列J 方程以用于计算未知的
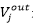
,其中j=1,…,J。
L%��.GKANM 下一步我们推导方程(10)的矩阵公式。为此,我们定义以下的矢量和矩阵:
:B'}#;8_�
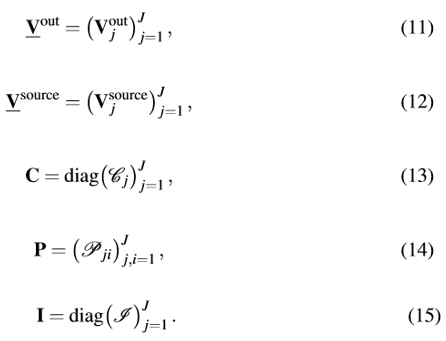 E$[\Fk�}�S 8_tMiIE-pS
E$[\Fk�}�S 8_tMiIE-pS I是恒等算子
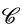
的对角矩阵。因为我们不考虑子域输出场到其自身输入场的映射,因此P的对角元素总是0。基于此定义我们重写了方程(10),其形式如下
-W+67@(\8H eM��vb*X6�  @.X}S�"yr� M�_4g%�uHG ]4>[y?�k34
@.X}S�"yr� M�_4g%�uHG ]4>[y?�k34 其将产生
�0fP��qO2 w�Q,��RZO3 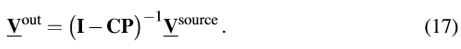 pTK|�u!�fs K/u`W�z�~A
pTK|�u!�fs K/u`W�z�~A 如果下列条件
E#Fy�L>:.h [�@= [<
_r  BKm$H!�u� f6Wu+�~�|Y
BKm$H!�u� f6Wu+�~�|Y 满足的话,则方程(17)可以很好的被定义并使用诺曼级数[7]来进行求解
�"/?*F�\5� $�{ ~U�A�6 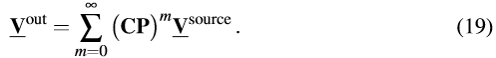 [#t����d� >1�tGQ
c�g
[#t����d� >1�tGQ
c�g 对广泛的应用来说,条件(18)是成立的。在介质中、外部边界处(无限)或者与探测器相连的边界处的任意吸收过程都会导致||CP||<1,因为||C||≤1且||P||≤1。然而,对于没有任何损耗的腔体,||CP||=1,因此,诺曼级数不会收敛。在这种情况下,分解和互联方法必须在一个本征求解器中使用。
�J7.bFW��' (19)中的级数极限是光学仿真问题的解。一个合适的截断可以用于近似解。很明显,连续的被加数可以通过一个更新后的公式进行计算。这种方法会导致一个所谓的光路树算法,我们将在下一部分讨论。为了进行求和计算,必须求解局部麦克斯韦问题以评估算子C和P。只要使用场矢量V的耦合确定了,任意严格或是近似的求解器的都能使用。这种方法称之为场追迹,我们将在第四部分进行讨论。
OR���^�Wd� y�=\�jQ6Fc 3. 光路树 ys�;e2xekg K0\a+��6kh 此部分我们将讨论如何有效地对方程(19)进行求解。为了避免重复相同的操作,我们将使用更新的公式。通过对无穷和进行截至,我们定义了一个迭代过程。第k次迭代的定义为
�%��1]2+_6 O`���dob&C  Co�1��9^g* 9hT^Y,c��0 h&� (@gU`A
Co�1��9^g* 9hT^Y,c��0 h&� (@gU`A 我们引入了一个辅助变量
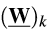
。然后,通过定义初始条件
]T(O;y*m � v�mO�XB#7W  )�B*?se]LJ }F�Ml4 _}u
)�B*?se]LJ }F�Ml4 _}u 我们获得了如下的更新公式
v�d /_`l.D ('uYA&�9�� 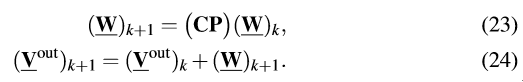 �]+�':=&+: �&bj :�,$@
�]+�':=&+: �&bj :�,$@ 给予一个阈值δ,一个合适的终止判据可由此定义
&u"*vG (U[ `z)�!���!y  i�m+2)9f�� BPr�A*u�}T
i�m+2)9f�� BPr�A*u�}T 其中rk是更新的
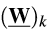
的相对功率:
i�:kWO�7aP P+3�G*M=}  0 �\�LkJ*i _�|TE )h��
0 �\�LkJ*i _�|TE )h�� 即使,为了求解矢量
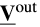
,我们已经定义了一个迭代过程。在每一步迭代中,我们必须求解多组局部麦克斯韦问题:一种是对每个子域Ωj(应用算子C);一种是对任意子域Ωi和Ωj(应用算子P)之间的每个自由空间区域。如果(18)成立,则结果将会收敛。我们将在第5部分给出了使用终止判据(25)获得的收敛结果。
uU.�9*B=H9 7�N�wi�\#o 事实证明更新公式(23)需要进行进一步的讨论。对某一行j 进行矩阵符号扩展,可以给出求和形式
� cJ8F#�t� 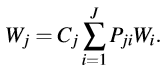 �?GFxJ6!%I d�0 V�>�;Q *-|+phi�m�
�?GFxJ6!%I d�0 V�>�;Q *-|+phi�m� 每个被加项都代表一个谐波场。为了利用那些勇于有效的构建子域求解器的场的局部特性,可取的的方法是不进行求和计算,而是在后续进行计算中操作单项被加数。
H�s=�!.tZ, u."fJ2}l0X 上述情况促使我们开发了光路树。这个算法能够考虑迭代矢量
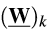
的稀疏性。这种稀疏性常见于光学模拟。实际上,这似乎有以下原因:(1)只有单个光源存在,(2)光沿一个路径传播通过元件(例如,在显微镜中经过一系列
透镜),(3)仅仅在表示探测器的一个(或者一些)平面上计算结果(例如,一个相机)。在[12]中已经讨论了序列场追迹(其中命名为“对流单邻近似”),对一个包含初始(光源)到终止(探测器)光路系统,它生成一个非零输入的
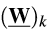
。这里,我们将这种方法推广到一般情况,我们也称之为非序列场追迹。
kM3BP&
3m1 HxY,�R��^ 举一个简单的例子,我们来讨论光路树的结构,这个例子是一个包含了一个光源、两个平板和一个用于计算光场的探测器的光学系统。装置如图3所示。
L''0`a. +S q��q�z�QKN 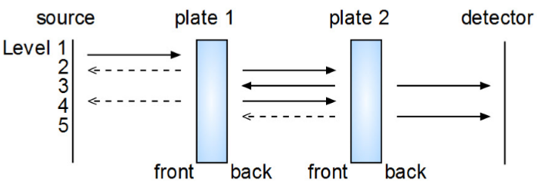 r$v?[x�>+K L�f�0H�z")
r$v?[x�>+K L�f�0H�z") 图3.包含一个光源,两个平板和一个探测器的光学系统的例子。箭头表示的是求和中的单个被加项,级次代表了计算截断求和的迭代步数。
1w�c
-v@�E P1��)
80<t 图3中,箭头表示光场在两个平板之间的传输。虚线箭头表示此传输对最终场没有贡献,即,可以将其忽略。此外,箭头按级次1至5进行排序。级次指数代表
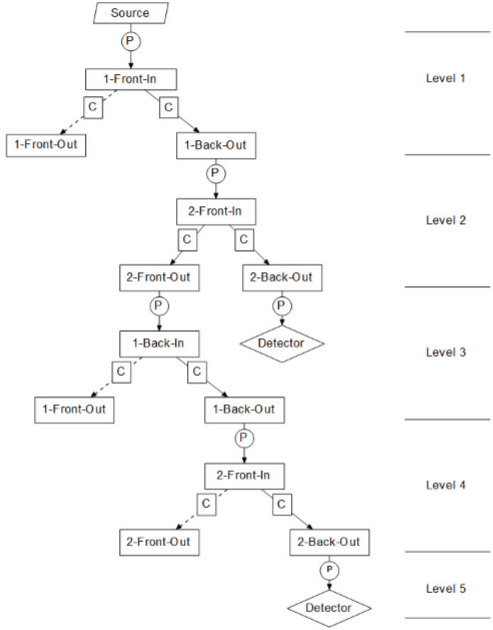
DAu|`pyC%� 7Xad2w�X�n DQlaSk4hF_ 了迭代数k。由于实际原因,我们为每个平板都引入了一个正面和背面。对如3中所描述的系统。对应的光路树如图4中所示。树的节点与任意矢量
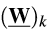
的一个输入(被加项)或者与在Γj处的解
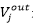
相联系。节点之间的联系与算子
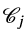
或者
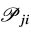
有关。不失一般性,我们假设
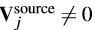
仅对一个指数j成立。因此,树仅有一个根节点。
f6�L_u�k`{ 忽略虚线链接,光路树对于计算截断总和是最合适的(20),因为其仅仅包含了那些必须的算符而相同的算符(求解相同的麦克斯韦问题两次)不会出现。
RaU.yCYyu� 8�nn�kv,wa 最后我们将讨论一个用于生自动生成光路树的算法。特别是我们想基于光线追迹近似使用试验光线来检测稀疏性。首先,我们引入一个数据集以来描述试验光线:
�m]-8?B1`Y Yn<0�D|S;X 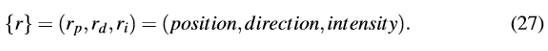 D�8�?$Fn=
D�8�?$Fn= 现在,对于试验光线,我们定义两类算子:(i)
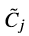
-对于在Γj上给定的试验光线,计算试验光线上域Ωj的效应。(ii)
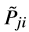
-对于在Γ_i上给定的试验光线,计算在Γi和Γj之间的自由空间的效应。
 Bd
Nuh�V`0
Bd
Nuh�V`0 图4.光路树用于两个平板的示例,其截断总和在k=5。
�l(]\[�}.5 �b(Z�%#*e� _kY�5���
6 此外,我们可以通过对试验光线使用强度规则来控制终止时机。为此,我们将光源的强度初始化为1。算子
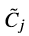
和
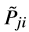
在处理强度时考虑了吸收效应、界面处的菲涅尔效应以及其他效应。对于一个给定的光源,我们定义树的根节点n^0并且指定初始试验光线强度为1。对于初始列表
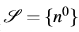
和一系列节点
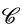
,用来构建树的算法AddNodes被递归调用。
z�t,-O7I'1 .v" lY2�:N 再次说明,条件(18)保证了树生成算法的终止。
ax^${s|�{- O�x~'w0c,f  qz0v�1057# .89�7Z|$VB 0X0D8H�(7Q 4.场追迹方法 #Y�5I_:k� 4{v�d6T}V!
qz0v�1057# .89�7Z|$VB 0X0D8H�(7Q 4.场追迹方法 #Y�5I_:k� 4{v�d6T}V! 在前面的部分我们已经描述了用于求解光学仿真任务的基于分解和互联技术的算法。已经表明,此算法需要两类算子。算子
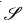
用于描述任意散射体间的自由空间传输,算子
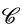
描述光学元件的散射效应。对于这些算子,仍然需要定义显式的公式。那么问题来了,
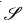
和
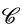
是否必须是严格的麦克斯韦方程求解器。如果是,此方法将会被限制在那些已知的物理光学上,包括最主流的如有限和边界元法,有限差分和有限积分技术。然而,经典光学建模和设计到现在已经使用时数十年了,从中我的知道,几何光学方法和其他的近似方法是及其强大的技术,能够描述自由空间传输
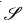
和各种重要的光学元件对谐波场的效应
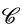
。由于光学系统的设计可以看做在特定条件下求解局部麦克斯韦问题,因此那些近似通常是有效的。对于此约束,一个经典的例子是在经典激光系统中发生的局部傍轴场。因此,实际经验非常鼓励我们使用不同的严格和近似局部麦克斯韦求解器以求解算子
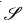
和
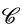
。用于一个系统子域的任何合适的建模技术都必须对电磁谐波场公式化。在此必须强调是,在过去这种方法并未在光学建模中成为标准。因此系统建模不是基于一种建模技术,而是多种建模技术的平滑结合,同时每个子域足够精确。这就是我们所说的统一化光学建模。在此方法中,根据之前给出的方程,谐波场以不同的算子
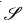
和
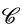
的形式被追迹通过系统。我们把这种方法称为场追迹,它是对光线追迹的自然推广,其中光线追迹是通过几何光学,追迹通过一个系统所有子域的光线束。总之,分解和互联算法,结合在不同的子域中针对
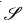
和
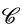
进行的谐波场技术的适当选择,实现了场追迹法统一化光学建模。在光学系统的建模中,生成的非序列场追迹概念是对非序列光线追迹本质的推广。
kuH;AM�d�v <�Y �or�Q> 对于算子
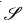
和
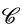
,已经在[12]中提出了一些可能的选择。其中,推导了几个自由空间算子并讨论了他们的近似特性。算子
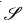
的一个严格版本可以从z=0处一个谐波场的平面波分解直接推导而来。这个分解过程可以描述为,将谐波场的任意分量傅里叶变换至k空间[1]:
KV5l�pN PC ��huF L� [  Q"�Ec7C5eM D+�SpSO7yg
Q"�Ec7C5eM D+�SpSO7yg 其中k=(kx,ky ),ρ=(x,y)且l=1,…,6。其逆变换如下:
i��`>X5Da5 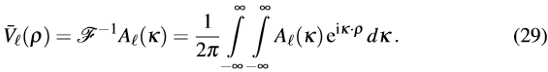 ?UfZ�VyHv+ �Y;&#Ur�8q i9xv`E�v=R
?UfZ�VyHv+ �Y;&#Ur�8q i9xv`E�v=R 对于平面波算子
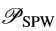
的推导,我们使用如下的事实,即每个平面波的传输通过乘以相位项
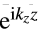
[2,5]进行描述。方向分量kz表示如下
d�JLJh*=AG lT�B!yF.r| 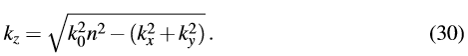 87^
��4",� 1!�f�'n�S
87^
��4",� 1!�f�'n�S 算子定义如下
jO,<7FP�s5 '!2t9�B8XX 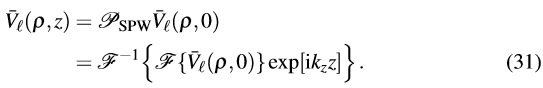 |��?|
�u-y ��l�lleo8
|��?|
�u-y ��l�lleo8 平面波角谱(SPW)算子没有引入物理近似。让我们来讨论其数值特性。光场分量的带宽在传输过程中是一个不变量。这可以从严格SPW算子(29)中推导出来。频谱乘以相位因子exp[ⅈkz]。这一步并不改变频谱的范围,也就是光场的带宽。基于采样原理[1],一个不变的带宽可以直接得出结论,即场的(最大)采样周期在传输中也是一个不变量。为了将(31)应用到一个采样场,需要两个离散傅里叶变换。对于采样点数N ,其数值计算量是接近最优的(O(NlogN))。采样点数是基于采样周期(传输过程中不变)以及输入和输出之间最大的场尺寸来定义的。因此,如果传输过程中场尺寸不明显变化的话,SPW算子会有一个接近最优的数值计算量。这种情况适用于小角度的傍轴场。然而,对于非傍轴场,用来评估结果的数值计算量变得不现实。在这种情况下,场尺寸在传输后可能比z=0处的场大的多。这就是为什么在可能的情况下必须使用相应的近似算子,,如适合于傍轴情况的菲涅尔算子或者适合于远场情况远场算子。在[12]中,已经显示了如何设计一个选择合适算子的自动程序以产生一个自动选择的自由空间传播算子。也可以使用快速边界元方法来替代。
�(t]>=p%4g ��*SY4lqN� 对于分量传输算子
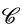
,几何光学方法被广泛的使用。关于他们的讨论,也可在[12]中发现。有限元微分法也可用于
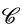
。为了理解有限元微分法,[8]中讨论了散射问题的公式化。让我们来简短的讨论一下效率问题。在场追迹的框架中,对一个子域生成的有限元系统,整个迭代过程保持不变。迭代进入边界条件,即,仅在方程的右边。在场追迹中迭代过程仅处理一次,而对于不同的右边部分,同样的系统需要进行多次求解。即,由于计算起来困难的矩阵分解可以被重复使用,因此使用直接求解器以求解有限元系统这种做法会非常高效。
ya_�'�Oz!C vv0zUvmT� 让我们在这里讨论一个关于算子
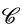
的特殊情况,即算子
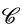
用于一个平面界面元件。我们考虑一个平面边界介于两种真实折射率为n_i和n_t的均匀介质间,它位于在z=0处。我们假设边界垂直于z轴。平面波在xz平面内传输,并假设以角度θ_i,从折射率为n_i的材料中入射。由于边界是无穷的,在xz平面内传输的单一反射和单一透射是通过相互作用产生的。波沿由角度θi和θt定义的方向传播。
2�T�3DV])Q �=P#!>*\ar 在准二维几何中,麦克斯韦方程组被分成可分别求解的两组。一组中仅包含y方向的电场(以及x方向和z方向的磁场),这一组讨论的是TE偏振。另外一组仅包含了y方向的磁场以及x和z方向的电场,然后这一组讨论的是TM偏振。两种偏振情况都能给出边界条件的一个直接评估。总之,例如,TE偏振以及通过
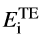
来表示入射光的复振幅,这个波可以使用如下形式来表示
y�Q�A[��X} (Z$6J�N�kz 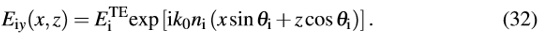 �Nb#7&_f�= V������1:3 P\��s�+2/�
�Nb#7&_f�= V������1:3 P\��s�+2/� 同理,振幅为
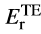
的反射光可以写为如下形式
Eo U�rc9G2 :7n��gVc� 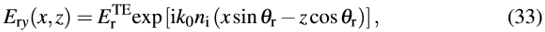 ��1�ZL_�;k �cLU*T�x\�
��1�ZL_�;k �cLU*T�x\� 我们已经注意到,光在入射介质中会反向传输。最后,复振幅为
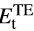
的透射光的表达式如下
�-$)Et���| ��i�f}]8�� 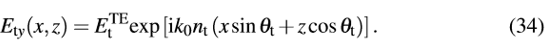 �cP2R2�4th �yy���} 0_
�cP2R2�4th �yy���} 0_ 接下来使用
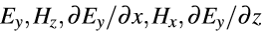
的连续条件,从而获得的决定反射和透射平面波自由参数的方程。在(x,z)=(0,0)处使用连续条件,推导出
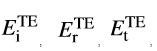
θi,θr和θt之间的三个方程,从中我们可以直接获得反射定律
o3yqG#d�A� K D-�_~uIF  7:L~�n(QpP 4s�j����%:
7:L~�n(QpP 4s�j����%: 以及斯涅尔折射定律
X}-�H�=1T? ���)/Xrhhx  |+:ZO5Fa�O �G�x!RaZ1�
|+:ZO5Fa�O �G�x!RaZ1� 其中定义了角度θt。此外,对于反射和折射场振幅,我们可以获得以下关系式
Tq�a4�~�|6 jp�^WsH�I3  Mdrv�/x�{ #P-���H�V�
Mdrv�/x�{ #P-���H�V� 以及
iy82QN��e m�G~y8nUtp 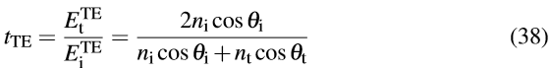 XC1lo���4| .:�ZX��t�U
XC1lo���4| .:�ZX��t�U 上述公式即是TE偏振光的菲涅尔方程。
ar��Ll8G[� 8~��)�[d!' 在此处给出的两个算子,用于下一部分中作为模型问题来讨论的平面界面问题。下一部分,我们将假设有一个傍轴设置,即θi=0。
y+scJ+�<�� I�Jc#)J.2A s�~$4bN>LD 5.数值案例 j$�|C/E5�? �0o|�,& K 在实际中,非序列场追迹算法的性能可以使用一个Fabry-Perot干涉仪系统来进行验证。特别是我们考虑一系列平行平板,如图5所示。我们再次引入了分解:一个平板分成两个边界。然后我们在均匀介质中(空气或者平板介质)应用平面波角谱算子并在每个边界使用(37)-(38)中的散射算子。
���*Z`eNz} ��r�g�z�I 图5.多平板实验装置。我们认为平板间的介质为空气(n=1),平板具的折射率n是一个变量。
�<M OL{jan
CDY�x/�yO 平板放置在空气中,空气折射率n=1.0027。在这个实验中,我们改变平板的折射率、平板数目以及平板厚度。平板的距离(如果超过一个)是5mm。我们使用了一个直径为几毫米的平面光源。实验中波长是变化的。不考虑吸收。
I���A`8ie+ 在第一个实验系列中,我们研究了算法的收敛性。为此,我们使用了试验光线算法,并观察了rk的收敛性(见(25))。结果见图6。
/�m�wr1GU� {}o>ne�nx\ 图6.不同设置的收敛结果:2个平板,折射率n=1.5(左图),2个平板,折射率n=3.0(中图)以及4个平板,折射率n=1.5(右图)。
1ys�L�Z;�K 我们考虑了两个平板(4个边界),其中n=1.5;两个平板(4个边界),其中n=3.0以及四个平板(8个边界),其中n=1.5。为了将误差降低到0.01,所需的迭代数分别为8(2个平板,n=1.5),13(2个平板,n=3)以及17(4个平板,n=1.5)。在第二个实验系列中,我们针对一些入射场使用了非序列场追迹算法,见图7。我们计算了不同装置的透射率。为了评价新的方法,我们使用一个严格的傅里叶模态法(FMM)[10],将两者的结果进行了对比。这种方法考虑的是周期性系统,并计算了一个无穷入射平面波的效率。FMM算法非常成熟,我们希望两种方法所计算出来的结果能够高度一致。
�\�u�i^
d /eRtj:�9�M ��.XKvk(�9 图7.左图,入射平面波(5mm直径)的振幅。右图,波长在400nm(n=1.4705)到600nm(n=1.4584)范围之间变化时Fused Silica的折射率。
$ Xs�Q ��e 在实验中我们也考虑了色散效应。当材料的折射率与波长相关时,即会产生这些效应。为此,我们使用Fused Silica作为平板材料。折射率如图7所示。我们再次改变一些系统的参数,考虑单个平板(2个边界)。在第一个系列中,我们将厚度作为变量,变化范围从1um到2um。
2M�l2Ue-9� 图8.单个fused silica平板的透过率。左图:波长为500nm,厚度在1um到2um之间变化。右图:厚度2um,波长在400nm(n=1.4705)到600nm(n=1.4584)范围之间变化。 在第二个系列中,波长在400nm到600nm之间变化。结果如图8所示。最后,我们对比了场追迹算法以及FMM的结果。
表1.场追迹方法与FMM所计算的透射率对比。
e�6i.�/bf3 结果如表1所示。正如期望一样,在所有的值之间可以看到一个非常好的吻合。
[E~�,��>�Q -mHhB�(Td' 6. 结论 ,�N7�l/6�� 我们展示了可用于光学仿真问题高效解答的光场追迹技术。由此生成的算法能够结合那些包含严格和近似方法的局部麦克斯韦求解器。在光学中,局部问题通常表现良好且局部求解器可以适应于局部特征以加快计算速度。进一步的实验检测并将这些局部特征进行分类。这些信息可以用于设计合适的局部求解器。此文章中所呈现的解算法可以很容易的并行运行。特别是一个树级次的所有局部求解器可以在一个分布计算环境下进行并行运行。然后,实现交流仅需要完成与子域边界相关的场数据的交换。尽管是为了将谐波场传播通过光学系统我们将场追迹公式化,但它也可以被用于一般场,如静态和脉冲光[9,11]。为此,一般场可以分解为一系列谐波场模式这些模式可以被追迹通过系统并使用合适的探测器进行评估。
<I�he�d��| 致谢:此处为Ulrich Langer学生,M.Kuhn博士的个人致谢。我总是乐于成为Ulrich Langer的学生和同事。我想要感谢他非凡的教育。Ulrich在表述科学问题方面具有卓越的能力,具有很强的实践意义。他鼓励我在麦克斯韦问题这个领域工作。最终,这引领我成为极具创新的光学仿真工具VirtualLab[6]
软件优秀开发团队的一员。我希望将此文章献给Ulrich。最后,他的前提“给需要解决的问题设置一个数学公式!”是这篇文章中所给出的结果的起点。最后但同样重要的是,没有我的合作作者以及LightTrans的同事,这篇文章是不可能完成的。
8�*#][�wC2 参考目录[1] Brigham, E.O.: The fast Fourier transform. Prentice-Hall, Englewood Cliffs (1974)
[�9U srpYi [2] Goodmann, J.W.: Introduction to Fourier optics. McGraw-Hill, New York (1968)[3] Langer, U., Steinbach, O.: Coupled boundary and finite element tearing and interconnecting methods. In Kornhuber, R., Hoppe, R., Periaux, J., Pironneau, O., Widlund, O.B., Xu, J. (eds.) Domain decomposition methods in science and engineering XV. Lecture Notes in Computational Sciences and Engineering, vol. 40, Springer, Heidelberg, pp. 83–97 (2003)
P�>T*:!s�; [4] Langer, U., Steinbach, O.: Coupled finite and boundary element domain decomposition methods. In Schanz, M., Steinbach, O. (eds.) Boundary Element Analysis. Mathematical Aspects and Applications. Lecture Notes in Applied and Computational Mechanics, vol. 29, Springer, Berlin, pp. 61–95 (2007) [5] Mandel, L., Wolf, E.: Optical coherence and quantum optics. Cambridge University Press, Cambridge (1995)
@�!a]qA�t� [6] LightTrans GmbH: VirtualLabTM - your optical modeling laboratory (2000– 2012,
http://www.lighttrans.com) [7] Meyer, C.D.: Matrix analysis and applied linear algebra, SIAM (2001)
e�AY�W%a�� [8] Monk, P.: Finite Element Methods for Maxwells Equations. Clarendon Press, Oxford (2003) [9] Tervo, J., Turunen, J., Wyrowski, F.: The Light Cube. In: 5th EOS Topical Meeting on Advanced Imaging Techniques, 3037. European Optical Society (2010)
�M}oj!�xGB [10] Turunen, J.: Diffraction theory of microrelief gratings. In Herzig, H.P. (ed.) Micro-optics elements, systems and applications. Taylor & Francis, London, pp. 31–52 (1997) [11] Wyrowski, F., Hellmann, C., Krieg, R., Schweitzer, H.: Modeling the propagation of ultrashort pulses through optical systems. In Neev, A., Nolte, J., Trebina,R.P.(eds.)Proc.SPIE,vol.7589,Heisterkamp,SanFrancisco(2010)
Px7�g�\�[] [12] Wyrowski, F., Kuhn, M.: Introduction to field tracing. J. Modern Optics 58(56 ):449–466 (2011)
xFm{oJ�!]& a�r��
qLp| QQ:2987619807