veIR�)i@dx
在JCMsuite中,利用光学手性的形式和内置的手性参量可以计算光散射体的手性响应。结果表明,时间谐波光学手性密度服从局部连续性方程[1]。这使得手性行为的分析类似于研究电磁能量的标准消光实验。 =
_X#�JP79
v]�SH�ude{
在电磁能量的情况下,消光由散射和损失[2]组成。对应的手性参量是光学手性的消光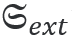 散射 散射 ,以及体积 ,以及体积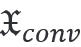 和界面上 和界面上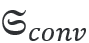 的手性转换。这就得到了守恒定律 S�{'�/=Px+ 的手性转换。这就得到了守恒定律 S�{'�/=Px+
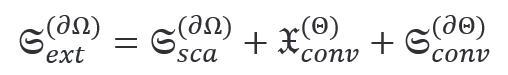 Y /$`vgqs� Y /$`vgqs�
积分是在散射体的外表面∂Ω和体积Θ以及表面∂Θ上进行的。 3om�Fd#E�P
�J6����J[\
这些参量在JCMsuite中命名,如下表所示。更多细节可以在这里找到。 +aR.t@D+"Y
o!!�";q%DX
作为案例展示,我们计算散射体的手性响应如下图所示: ���&.J�8O+
&D0s�u�K#
它的直径是一个波长的量级,它的介电常数固定为ε=4.5。在下面,我们将改变散射体的磁导率μ,并观察预测的对偶对称性[3]对于恒定比率ε/μ的散射体及其环境。周围的材料是ε=μ=1的空气。 zO8`��xrN!
由于散射体是无损的和各向同性的,在它的体积内将没有转换。请参考四分之一波片的案例,以获得更多关于体积转换的信息。 __o`+�^FS�
在这里,所需的参量被计算为如上所述的电磁手性通量的通量积分。如下图所示,对于接近对偶对称的材料,转换趋向于零。 8|*#r���[x
在固定介电常数ε=4.5下,散射体的磁导率μ的变化。 该散射体是对偶的ε/μ=1,产生零手性转换。 ��>oSN�KE
golr,+LSo�
在JCMsuite中,所有手性密度都是相似的。例如,我们在下面的图中展示了增强的近场光学手性密度的电子部分。这是一个后处理过程,即ExportFields:输出参量电手性密度。 �"h?;�)Ye�
具有ε/μ=1的双散射体的光手性密度X的近场增强 �b~dm+5�W7
D�#Fe\8!�l
参考文献 db#QA#��^S
[1] Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756m pages 97560X. International Society for Optics and Photonics, 2016. M0VC-\W7f
[2] Craig F. Bohren and Donald R. Huffman. Absorption and Scattering of Light by Small Particles. John Wiley & Sons, 1940. o>*��v�G�
[3] Ivan Fernandez-Corbaton. Helicity and duality symmetry in light matter interactions: Theory and applications. PhD thesis, Macquarie University, Department of Physics and Astronomy, 2014. |