| infotek | 2023-08-24 08:26 |
OptiSystem应用:光纤陀螺仪系统设计使用理想元件,输出光电流(I)为 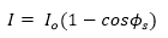 (1) (1) 其中 φs 是萨格纳克相移 , Io 是以零角速度情况计算出的电流 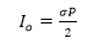 (2) (2) P 是光源光功率, σ 是光电检测器的响应度(在我们的案例中等于1)。在等式(2)中将光功率除以2是因为在耦合器处功率损失了一半。 一旦 φs 确定了, 我们可以计算 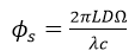 (3) (3) 其中 L 是光线长度, D 是环直径, λ 是光源波长,由此来确定环路Ω 的角速度。注意,由于等式(1)具有余弦,因此直流技术无法区分正负速度。 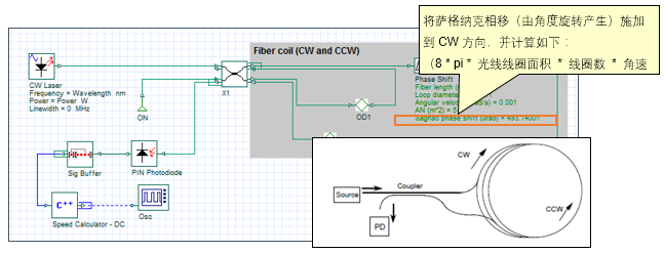 图1.FOG DC检测布局 光纤陀螺仪系统设计:相位调制方法[2] 当尝试测量非常低的角旋转速率时,DC方法不是很准确,所以通常使用相位调制技术。 对于该设置,光检测信号 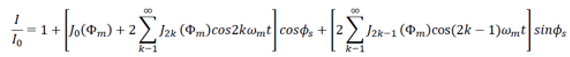 (4) (4) 将相位调制器幅度选择到+/-0.9 rad ,给出最大化J1(Φm) = 0.581517 的项Φm = 1.8 。提取调制频率ωm的余弦级数 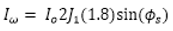 (5) (5) 公式3得到角速度。我们可以重新排列找到φ_𝑠,然后再次使用公式(3)找到角速度。 注意,在这种情况下,由于等式(5)具有正弦关系,所以我们可以确定角速度的大小和方向。另外,在这种情况下, 在等式(2)中,零速电流不是𝐼_𝑜=𝜎𝑃/2 而是 𝐼_𝑜=𝜎𝑃/8因为在光到达光电二极管的时候,其功率已经被耦合器减半了三次。 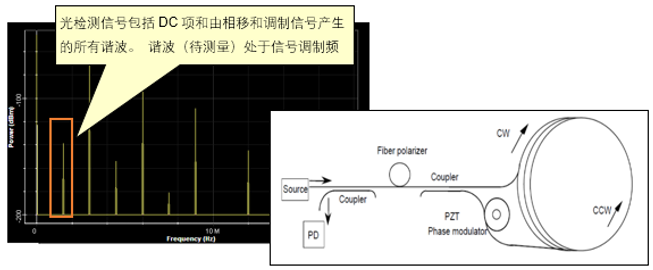 图2.OptiSystem设计的调制技术原理图(资料来源:REF)(注:光纤偏振器未包含在设计中) 对于以下的OptiSystem设计,角速度已设置为7.27e-5rad / s(地球的转速)。 I-FOG的设置显示在红色框中(在全局参数下)。 通过使用相移分量来应用萨格纳克相移,计算如下: 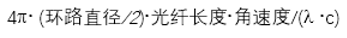 在这里,我们根据前面的方程,使用C ++组件来计算角速度。 测得的角速度(在C ++组件下显示为结果)为7.29e-5rad / s。  图3.FOG 相位调制 |
|